题目内容
(本题13分)
已知函数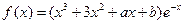 .
.
(1)当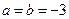 时,求
时,求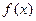 的单调区间;
的单调区间;
(2)若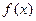 在
在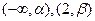 单调增加,在
单调增加,在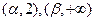 单调减少,证明:
单调减少,证明: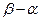 <6.
<6.
已知函数
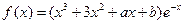 .
.(1)当
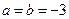 时,求
时,求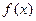 的单调区间;
的单调区间;(2)若
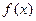 在
在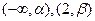 单调增加,在
单调增加,在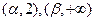 单调减少,证明:
单调减少,证明: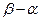 <6.
<6.解:(1)当
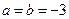 时,
时, ,故
,故
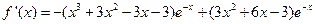
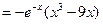
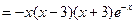
当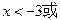
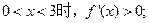 当
当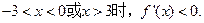
从而 单调减少.----(6分)
单调减少.----(6分)
(2)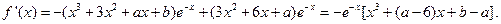
由条件得: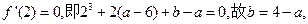
从而
因为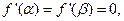
所以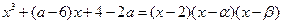
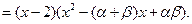
将右边展开,与左边比较系数得,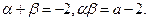
故
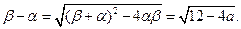
又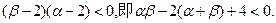
由此可得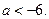 于是
于是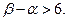 --------------------(13分)
--------------------(13分)

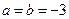 时,
时, ,故
,故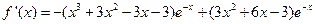
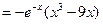
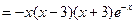
当
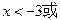
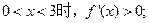 当
当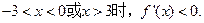
从而
 单调减少.----(6分)
单调减少.----(6分)(2)
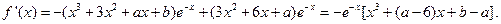
由条件得:
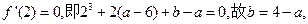
从而

因为
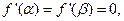
所以
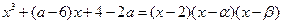
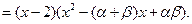
将右边展开,与左边比较系数得,
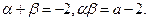
故

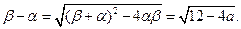
又
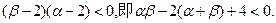
由此可得
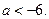 于是
于是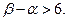 --------------------(13分)
--------------------(13分)略

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
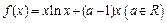 .
.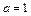 时,求曲线
时,求曲线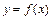 在
在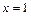 处的切线方程;
处的切线方程;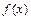 在区间
在区间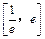 上的最小值;
上的最小值;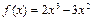 在区间
在区间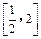 内有两个不相等的实数根,求实数a的取值范围.
内有两个不相等的实数根,求实数a的取值范围.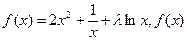 的导数是
的导数是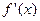 .
.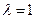 时,
时,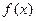 在x=1处的切线方程。
在x=1处的切线方程。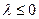 时,求证:对于任意的两个不等的正数
时,求证:对于任意的两个不等的正数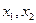 ,有
,有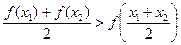 ;
;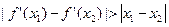 恒成立,求
恒成立,求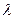 的取值范围.
的取值范围.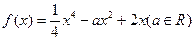 .
.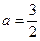 ,求函数
,求函数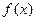 极值;
极值;  ,若函数F(x)在[0,1]上单调递增,求
,若函数F(x)在[0,1]上单调递增,求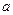 的取值范围.
的取值范围.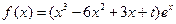 ,
,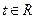 .依次在
.依次在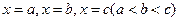 处取到极值.
处取到极值.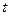 的取值范围;
的取值范围;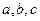 成等差数列,求
成等差数列,求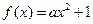 ,若
,若 ,则
,则 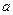 =" " ;
=" " ;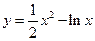 的单调递减区间为 ▲ .
的单调递减区间为 ▲ . 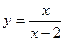 在点(1,-1)处的切线方程为 ( )
在点(1,-1)处的切线方程为 ( )