题目内容
已知函数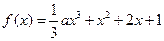 .
.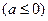
(Ⅰ)求函数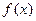 在
在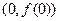 处的切线方程;
处的切线方程;
(Ⅱ)若函数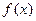 在
在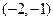 上单调减,且在
上单调减,且在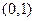 上单调增,求实数
上单调增,求实数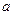 的取值范围;
的取值范围;
(Ⅲ)当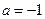 时,若
时,若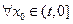 ,函数
,函数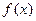 的切线中总存在一条切线与函数
的切线中总存在一条切线与函数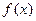 在
在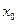 处的切线垂直,求
处的切线垂直,求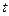 的最小值.
的最小值.
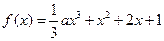 .
.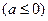
(Ⅰ)求函数
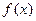 在
在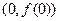 处的切线方程;
处的切线方程;(Ⅱ)若函数
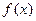 在
在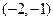 上单调减,且在
上单调减,且在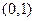 上单调增,求实数
上单调增,求实数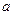 的取值范围;
的取值范围;(Ⅲ)当
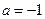 时,若
时,若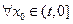 ,函数
,函数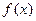 的切线中总存在一条切线与函数
的切线中总存在一条切线与函数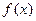 在
在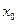 处的切线垂直,求
处的切线垂直,求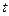 的最小值.
的最小值.解:(I)由已知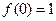 ,
,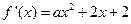 ,所以
,所以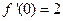 ,
,
所以函数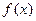 在
在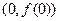 处的切线方程为
处的切线方程为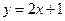
(II)解1:①当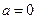 时,
时, ,满足在
,满足在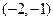 上
上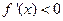 ,且在
,且在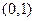 上
上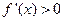 ,所以当
,所以当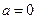 时满足题意;
时满足题意;
②当 时,
时,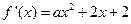 是恒过点
是恒过点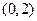 ,开口向下且对称轴
,开口向下且对称轴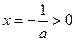 的抛物线,由二次函数图象分析可得在
的抛物线,由二次函数图象分析可得在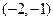 上
上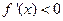 ,且在
,且在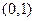 上
上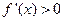 的充要条件是
的充要条件是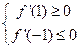 解得
解得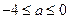 ,即
,即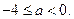
综上讨论可得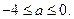
解2:由已知可得在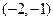 上
上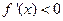 ,且在
,且在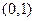 上
上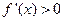 ,
,
即 在
在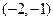 上成立且
上成立且 在
在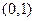 成立;
成立;
因为在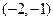 上
上 ,在
,在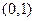 上
上
所以
(III)当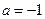 时,
时,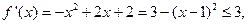
由题意可得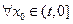 ,总存在
,总存在 使得
使得 成立,即
成立,即
 成立,因为
成立,因为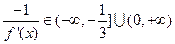 ,当
,当 时,
时,
 ,所以
,所以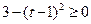 ,解得
,解得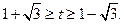
所以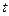 的最小值为
的最小值为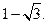
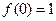 ,
,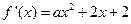 ,所以
,所以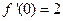 ,
,所以函数
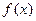 在
在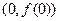 处的切线方程为
处的切线方程为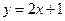
(II)解1:①当
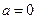 时,
时, ,满足在
,满足在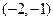 上
上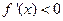 ,且在
,且在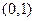 上
上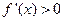 ,所以当
,所以当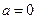 时满足题意;
时满足题意;②当
 时,
时,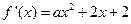 是恒过点
是恒过点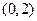 ,开口向下且对称轴
,开口向下且对称轴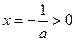 的抛物线,由二次函数图象分析可得在
的抛物线,由二次函数图象分析可得在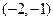 上
上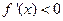 ,且在
,且在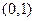 上
上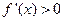 的充要条件是
的充要条件是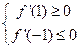 解得
解得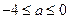 ,即
,即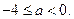
综上讨论可得
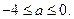
解2:由已知可得在
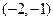 上
上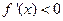 ,且在
,且在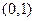 上
上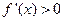 ,
,即
 在
在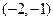 上成立且
上成立且 在
在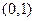 成立;
成立;因为在
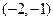 上
上 ,在
,在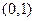 上
上
所以

(III)当
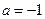 时,
时,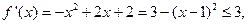
由题意可得
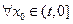 ,总存在
,总存在 使得
使得 成立,即
成立,即 成立,因为
成立,因为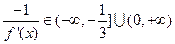 ,当
,当 时,
时, ,所以
,所以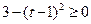 ,解得
,解得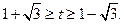
所以
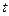 的最小值为
的最小值为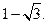
略

练习册系列答案
相关题目
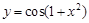 的导数是( )
的导数是( ) B.
B.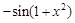 C.
C. D.
D.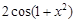
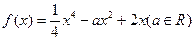 .
.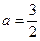 ,求函数
,求函数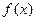 极值;
极值;  ,若函数F(x)在[0,1]上单调递增,求
,若函数F(x)在[0,1]上单调递增,求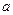 的取值范围.
的取值范围.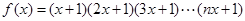 ,则
,则 ( )
( )
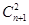
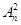

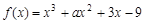 ,已知
,已知 在
在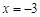 时取极值,则a=
时取极值,则a= -x (e为自然对数的底数).
-x (e为自然对数的底数).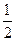 ≤x≤2}且M∩P≠
≤x≤2}且M∩P≠ ,求实数a的
,求实数a的 =
=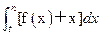 (t为常数,t≥0),是否存在等比数列{
(t为常数,t≥0),是否存在等比数列{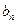 },使得b1+b2+…
},使得b1+b2+…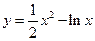 的单调递减区间为 ▲ .
的单调递减区间为 ▲ . 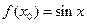 ,
,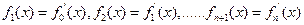
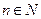 ,则
,则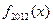 等于( )
等于( ) x
x