题目内容
10．设复数z1，z2满足条件|z1|=1，|z2|=2，则|z1-z2|的范围是[1，3]．分析 直接利用复数的模的几何意义，判断求解即可．
解答 解：复数z1，z2满足条件|z1|=1，|z2|=2，说明两个复数的对应点是两个同心圆，半径分别为1，2，
|z1-z2|的范围是：[1，3]．
故答案为：[1，3]．
点评 本题考查复数的模的几何意义，基本知识的考查．
练习册系列答案
相关题目
10．设 Pn（xn，yn）是直线2x-y=$\frac{n}{n+1}$（n∈N*）与圆x2+y2=2在第一象限的交点，则极限$\lim_{n→∞}\frac{{{y_n}-1}}{{{x_n}-1}}$=（ ）
| A． | -1 | B． | -$\frac{1}{2}$ | C． | 1 | D． | 2 |
1．给出下列两个推理：
①在△ABC中，若D为BC的中点，则$\overrightarrow{AD}$=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$），由此推测：在空间四面体ABCD中，若M为△BCD的重心，则$\overrightarrow{AM}$=$\frac{1}{3}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$+$\overrightarrow{AD}$）．
②无根不循环小数都是无理数，因为e=2.7182818459045…是无限不循环小数，所以e是无理数．
对于上述两个推理，下列判断正确的是（ ）
①在△ABC中，若D为BC的中点，则$\overrightarrow{AD}$=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$），由此推测：在空间四面体ABCD中，若M为△BCD的重心，则$\overrightarrow{AM}$=$\frac{1}{3}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$+$\overrightarrow{AD}$）．
②无根不循环小数都是无理数，因为e=2.7182818459045…是无限不循环小数，所以e是无理数．
对于上述两个推理，下列判断正确的是（ ）
| A． | ①是类比推理，②是归纳推理 | B． | ①是类比推理，②是演绎推理 | ||
| C． | ①是归纳推理，②是演绎推理 | D． | ①是演绎推理，②是类比推理 |
5．
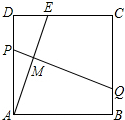在祖国60年国庆庆典晚会上，需制作表演道具，如图．将一块边长为12的正方形纸ABCD的顶点A折叠至边上的点E，使DE=5，折痕为PQ，则线段PM和MQ的比是（ ）
在祖国60年国庆庆典晚会上，需制作表演道具，如图．将一块边长为12的正方形纸ABCD的顶点A折叠至边上的点E，使DE=5，折痕为PQ，则线段PM和MQ的比是（ ）| A． | 5：12 | B． | 5：13 | C． | 5：19 | D． | 5：21 |
15．已知a＞0且a≠1，命题“?x＞1，logax＞0”的否定是（ ）
| A． | ?x≤1，logax＞0 | B． | ?x＞1，loga≤0 | C． | ?x≤1，logax＞0 | D． | ?x＞1，logax≤0 |