题目内容
19.在数列{an}中,Sn为它的前n项和,已知a2=3,a3=7,且数列{an+1}是等比数列,则a1=1,an=2n-1,Sn2n+1-2-n.分析 利用a2=3,a3=7,且数列{an+1}是等比数列,可得a1+1=2,所以a1=1,确定an+1=2n,可得an=2n-1,利用等比数列的求和公式,即可得出结论.
解答 解:因为a2=3,a3=7,且数列{an+1}是等比数列,
所以a1+1=2,所以a1=1,
an+1=2n,所以an=2n-1,
所以Sn=$\frac{2(1-{2}^{n})}{1-2}$-n=2n+1-2-n.
故答案为:1,2n-1,2n+1-2-n.
点评 本题考查等比数列的通项与求和,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
4.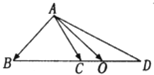 在△ABC中,点D在线段BC的延长线上,且$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围是( )
在△ABC中,点D在线段BC的延长线上,且$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围是( )
 在△ABC中,点D在线段BC的延长线上,且$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围是( )
在△ABC中,点D在线段BC的延长线上,且$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围是( )| A. | (-1,0) | B. | (0,$\frac{1}{3}$) | C. | (0,1) | D. | (-$\frac{1}{3}$,0) |
11.在△ABC中,内角A,B,C所对应的边分别为a,b,c,若bsinA-$\sqrt{3}$acosB=0,且b2=ac,则$\frac{b}{a+c}$的值为
( )
( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
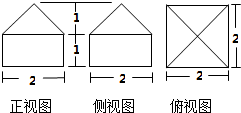 已知一几何体的三视图如图所示.
已知一几何体的三视图如图所示.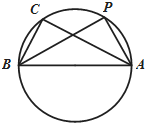 在△ABC中,三个内角A,B,C的对边分别为a,b,c,其中c=2,且$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\frac{\sqrt{3}}{1}$.
在△ABC中,三个内角A,B,C的对边分别为a,b,c,其中c=2,且$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\frac{\sqrt{3}}{1}$.