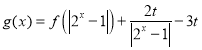题目内容
【题目】红队队员甲、乙、丙与蓝队队员
，
，
进行围棋比赛，甲对，乙对，丙对各一盘.已知甲胜、乙胜、丙胜的概率分别为0.6，0.5，0.5，假设各盘比赛结果相互独立，则红队至少两名队员获胜的概率是____________.
【答案】0.55
【解析】
根据题意，可知红队至少两名队员获胜的情况有：①甲和乙胜，丙败；②甲和丙胜，乙败；③乙和丙胜，甲败；④甲、乙、丙都胜；根据分步乘法的计数原理分别求出每种情况的概率，最后再利用分类加法的计数原理求出结果.
解：由题可知，各盘比赛结果相互独立，则红队至少两名队员获胜的情况有：
①甲和乙胜，丙败；②甲和丙胜，乙败；③乙和丙胜，甲败；④甲、乙、丙都胜；
而甲胜
、乙胜
、丙胜
的概率分别为0.6，0.5，0.5，
则①甲和乙胜，丙败的概率为：
，
②甲和丙胜，乙败的概率为：，
③乙和丙胜，甲败的概率为：
，
④甲、乙、丙都胜的概率为：
，
则红队至少两名队员获胜的概率为：
.
故答案为：0.55.
【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在
内，发布成绩使用等级制，各等级划分标准见下表．
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定：A，B，C三级为合格等级，D为不合格等级为了解该校高三年级学生身体素质情况，从中抽取了n名学生的原始成绩作为样本进行统计．
按照
，
，
，
，
的分组作出频率分布直方图如图1所示，样本中分数在80分及以上的所有数据的茎叶图如图2所示
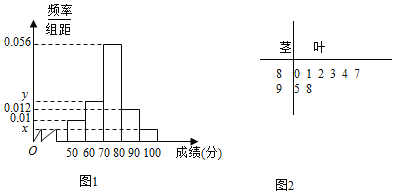
求n和频率分布直方图中的x，y的值，并估计该校高一年级学生成绩是合格等级的概率；
根据频率分布直方图，求成绩的中位数
精确到
；
在选取的样本中，从A，D两个等级的学生中随机抽取2名学生进行调研，求至少有一名学生是A等级的概率．
【题目】省环保厅对
、
、
三个城市同时进行了多天的空气质量监测，测得三个城市空气质量为优或良的数据共有180个，三城市各自空气质量为优或良的数据个数如下表所示：
|
|
| |
优（个） | 28 |
|
|
良（个） | 32 | 30 |
|
已知在这180个数据中随机抽取一个，恰好抽到记录
城市空气质量为优的数据的概率为0.2.
（1）现按城市用分层抽样的方法，从上述180个数据中抽取30个进行后续分析，求在
城中应抽取的数据的个数；
（2）已知
， 
，求在
城中空气质量为优的天数大于空气质量为良的天数的概率.
