Question

【题目】已知直线： ， ： ，动点分别在直线， 上移动， ， 是线段的中点.

（1）求点的轨迹的方程；

（2）设不经过坐标原点且斜率为的直线交轨迹于点，点满足，若点在轨迹上，求四边形的面积.

Answer 1

【答案】（I）. （II）见解析.

【解析】试题分析：（1）根据条件设， ， ，即. 设，由中点坐标公式消去参数m,n得 .

（2）设直线的方程为， ， ， .将代入，整理得 .则 ， . 因为，可得R(， . 由在椭圆上，有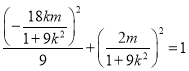，化简得. 从而整理可得 . 可求得四边形的面积.

试题解析：（1）根据条件可设， ，由，得:

.

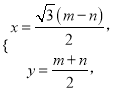设，则得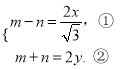

将①和②代入中并化简得： .

所以点的轨迹的方程为.

（2）设直线的方程为， ， ， .

将代入，整理得 .

则 ， .

.

因为，则有： ， .

因为在椭圆上， ，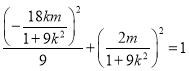

化简得： .

所以， ，

因为

.

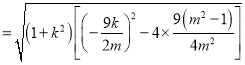
又点到的距离为.

由，可知四边形为平行四边形，

.

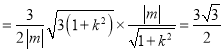拓展: 此题结论可推广到更一般情形:

第(Ⅰ))题中, 直线、只要不垂直,轨迹均为椭圆, 、垂直时,轨迹为圆;

第(Ⅱ)题中结论可推广到更一般情形:

设不经过坐标原点且斜率为的直线交椭圆: 于点、，点满足. 若点在椭圆上，则四边形OPRQ(或)的面积为定值。