Question

【题目】已知函数关于x的函数.

（1）当时，求的值域；

（2）若不等式对恒成立，求实数m的取值范围；

（3）若函数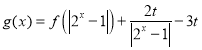有3个零点，求实数t的取值范围.

Answer 1

【答案】（1）（2）（3）

【解析】

（1）首先根据对勾函数的单调性得到的单调性，结合定义域即可得值域；

（2）利用分离参数思想得出恒成立，求不等式右边的最小值即可；

（3）设，换元转化为方程的根的范围问题，再用根的分布方法求解.

（1）函数在上单调递减，在上单调递增；

又，；

故的值域为；

（2）不等式对恒成立；

即，则；

∵，∴

故实数m的取值范围：；

（3）根据题意有，则；

设，则；

由条件有3个零点，则

即方程有两个不等实数根；

且两个根，满足：，；

设函数

当时，，此时不满足条件；

∴，则；

故实数t的取值范围：.