题目内容
6.某几何体的三视图如图所示,则该几何体的体积为$\frac{13}{2}$
分析 根据几何体的三视图得出该几何体是一个正方体切去两个三棱锥所得的组合体,分别求出它们的体积,相减可得答案.
解答 解:根据几何体的三视图得出该几何体是一个正方体切去两个三棱锥所得的组合体,
其直观图如下所示: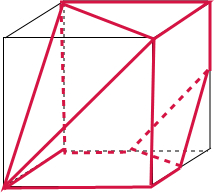
正方体的棱长为2,故体积为8,
切去的大三棱锥的体积为:$\frac{1}{3}×\frac{1}{2}×2×2×2$=$\frac{4}{3}$,
切去的小三棱锥的体积为:$\frac{1}{3}×\frac{1}{2}×1×1×1$=$\frac{1}{6}$,
故组合体的体积V=8-$\frac{4}{3}$-$\frac{1}{6}$=$\frac{13}{2}$,
故答案为:$\frac{13}{2}$
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示为1984年到2008年的奥运会中,我国每届奥运会获得的金牌数,设年份为x(x∈{1984,1988,1992,1996,2000,2004,2008}),金牌数为y,试判断y是否为x的函数,x是否为y的函数.
如图所示为1984年到2008年的奥运会中,我国每届奥运会获得的金牌数,设年份为x(x∈{1984,1988,1992,1996,2000,2004,2008}),金牌数为y,试判断y是否为x的函数,x是否为y的函数.