题目内容
17.已知关于x的不等式x2-bx-2a<0的解集为(-1,3).(1)求不等式x2-x-b>0的解集;
(2)设变量x,y满足不等式$\left\{\begin{array}{l}{{x}^{2}-2ax+b≤0}\\{x-y+1≥0}\\{2x+3y≥6}\end{array}\right.$,求目标函数z=2x+y的取值范围.
分析 由已知不等式的解集得到对应的一元二次方程的解,进一步求出a,b,然后继续解不等式以及线性规划的问题.
解答 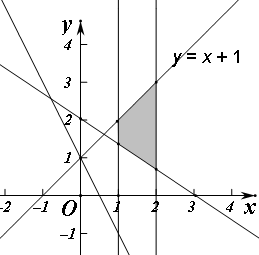 解:因为关于x的不等式x2-bx-2a<0的解集为(-1,3).
解:因为关于x的不等式x2-bx-2a<0的解集为(-1,3).
所以x2-bx-2a=0的解为-1,3,所以b=2,a=$\frac{3}{2}$,
所以(1)不等式x2-x-b>0为x2-x-2>0,它的解集为(-∞,-1)∪(2,+∞);
(2)设变量x,y满足不等式为$\left\{\begin{array}{l}{{x}^{2}-3x+2≤0}\\{x-y+1≥0}\\{2x+3y≥6}\end{array}\right.$,即$\left\{\begin{array}{l}{1≤x≤2}\\{x-y+1≥0}\\{2x+3y≥6}\end{array}\right.$,
对应的平面区域如图:
由$\left\{\begin{array}{l}{2x+3y=6}\\{x=1}\end{array}\right.$得到(1,$\frac{4}{3}$),
由$\left\{\begin{array}{l}{y=x+1}\\{x=2}\end{array}\right.$得到(2,3),由图形得知,目标函数z=2x+y在(1,$\frac{4}{3}$)处得到最小值为2×1+$\frac{4}{3}$=$\frac{10}{3}$,在(2,3)出得到最大值为2×2+3=7,
所以目标函数z=2x+y的取值范围为[$\frac{10}{3}$,7].
点评 本题考查了一元二次不等式的解集与对应的方程根的关系以及简单的线性规划问题;体现了待定系数法和数形结合的思想.

练习册系列答案
相关题目