��Ŀ����
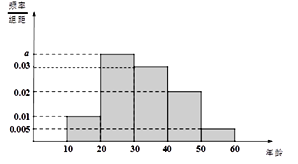
����Ŀ����ijУ�����꼶ѧ���μ����������������ͳ�ƣ������ȡM��ѧ����Ϊ�������õ���M��ѧ���μ���������Ĵ��������ݴ�����������Ƶ����Ƶ�ʵ�ͳ�Ʊ����£�Ƶ�ʷֲ�ֱ��ͼ��ͼ��
���� | Ƶ�� | Ƶ�� |
[10��15�� | 10 | 0.25 |
[15��20�� | 24 | n |
[20��25�� | m | p |
[25��30�� | 2 | 0.05 |
�ϼ� | M | 1 |

��1���������M��p��ͼ��a��ֵ��
��2������У����ѧ����240�ˣ��Թ��Ƹ�У����ѧ���μ���������Ĵ���������[10��15���ڵ�������
��3������ȡ�����У��Ӳμ���������Ĵ���������20�ε�ѧ������ѡ2�ˣ�������һ�˲μ������������������[25��30���ڵĸ��ʣ�
���𰸡���1��![]() �� ��2��60�� ��3��
�� ��2��60�� ��3��![]()
��������
��1������Ƶ�ʣ�Ƶ������������֮��Ĺ�ϵ��Ƶ�ʵ���Ƶ����������������д����ʽ�����ʽ���е���ĸ��ֵ����2�����ݸ�У����ѧ����240�ˣ�����[10��15���ڵ�Ƶ����0.25�����Ƹ�У����ѧ���μ���������Ĵ����ڴ������ڵ�����Ϊ60�ˣ���3����������μ���������Ĵ���������20�ε�ѧ������m+2��6�ˣ����������[20��25���ڵ���Ϊa1��a2��a3��a4��������[25��30���ڵ���Ϊb1��b2���оٳ������¼��������������¼����õ����ʣ�
��1���ɷ���[10��15���ڵ�Ƶ����10��Ƶ����0.25֪��![]() ��
��
��M��40��
��Ƶ��֮��Ϊ40��
��10+24+m+2��40��m��4.![]() ��
��
��a�Ƕ�Ӧ����[15��20����Ƶ���������̣�
��![]()
��2����Ϊ��У����ѧ����240�ˣ�����[10��15���ڵ�Ƶ����0.25��
����Ƹ�У����ѧ���μ���������Ĵ����ڴ������ڵ�����Ϊ60�ˣ�
��3����������μ���������Ĵ���������20�ε�ѧ������m+2��6�ˣ�
��������[20��25���ڵ���Ϊa1��a2��a3��a4��������[25��30���ڵ���Ϊb1��b2��
����ѡ2�˹��У�a1��a2������a1��a3������a1��a4������a1��b1������a1��b2������a2��a3������a2��a4������a2��b1������a2��b2������a3��a4������a3��b1������a3��b2������a4��b1������a4��b2������b1��b2��15�������
�����˶���[25��30����ֻ���ǣ�b1��b2��һ�֣�
���������Ϊ![]() ��
��

 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�