题目内容
16.已知数列{an}满足an+1=$\frac{1}{{1-{a_n}}}$,若a1=$\frac{1}{2}$,则a2015=( )| A. | 2 | B. | -2 | C. | -1 | D. | $\frac{1}{2}$ |
分析 通过求出前几项的值得出该数列是以3为周期的周期数列,进而可得结论.
解答 解:∵an+1=$\frac{1}{{1-{a_n}}}$,a1=$\frac{1}{2}$,
∴a2=$\frac{1}{1-{a}_{1}}=\frac{1}{1-\frac{1}{2}}$=2,
a3=$\frac{1}{1-{a}_{2}}=\frac{1}{1-2}=-1$,
a4=$\frac{1}{1-{a}_{3}}=\frac{1}{1-(-1)}=\frac{1}{2}$,
∴数列{an}是以3为周期的周期数列,
∵2015=671×3+2,
∴a2015=a2=2,
故选:A.
点评 本题考查数列的通项,求出周期是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
7.如图在区域Ω={(x,y)|-2≤x≤2,0≤y≤4}中随机撒900粒豆子,如果落在每个区域的豆子数与这个区域的面积近似成正比,试估计落在图中阴影部分的豆子数为( )
| A. | 300 | B. | 400 | C. | 500 | D. | 600 |
11.下列命题中正确的是( )
| A. | 类比推理是一般到特殊的推理 | |
| B. | 演绎推理的结论一定是正确的 | |
| C. | 合情推理的结论一定是正确的 | |
| D. | 演绎推理在前提和推理形式都正确的前提下,得到的结论一定是正确的 |
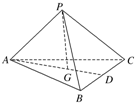 在三棱锥PABC中,G为△ABC的重心,设$\overrightarrow{PA}$=a,$\overrightarrow{PB}$=b,$\overrightarrow{PC}$=c,则$\overrightarrow{PG}$=$\frac{1}{3}$($\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$)(用a,b,c表示).
在三棱锥PABC中,G为△ABC的重心,设$\overrightarrow{PA}$=a,$\overrightarrow{PB}$=b,$\overrightarrow{PC}$=c,则$\overrightarrow{PG}$=$\frac{1}{3}$($\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$)(用a,b,c表示).