题目内容
某高校从今年参加自主招生考试的学生中随机抽取容量为 的学生成绩样本,得到频率分布表如下:
的学生成绩样本,得到频率分布表如下:
| 组数 | 分组 | 频数 | 频率 |
| 第一组 | [230,235) | 8 | 0.16 |
| 第二组 | [235,240) |  | 0.24 |
| 第三组 | [240,245) | 15 |  |
| 第四组 | [245,250) | 10 | 0.20 |
| 第五组 | [250,255] | 5 | 0.10 |
| 合计 |  | 1.00 | |
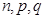 的值;
的值;(2)为了选拔出更加优秀的学生,该高校决定在第三、四、五组中用分层抽样的方法抽取6名学生进行第二轮考核,分别求第三、四、五组参加考核的人数;
(3)在(2)的前提下,高校决定从这6名学生中择优录取2名学生,求2人中至少有1人是第四组的概率.
(1)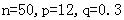 (2)3,2,1 (3)
(2)3,2,1 (3)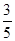
解析试题分析:(1)由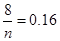 得n=50;由
得n=50;由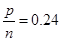 得
得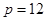 ,
,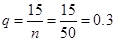 (2)根据各组占总数的百分比抽取即可(3)从这6名学生中取2名学生的取法总数n=
(2)根据各组占总数的百分比抽取即可(3)从这6名学生中取2名学生的取法总数n=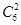 =15,2人中至少有1人是第四组的取法有
=15,2人中至少有1人是第四组的取法有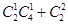 =9,根据随机事件的概率公式求之即可.
=9,根据随机事件的概率公式求之即可.
试题解析: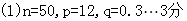
(2)第三组取3人,第四组取2人,第五组取1人, 6分
(3)从这6名学生中取2名学生的取法总数n=15,2人中至少有1人来自第四组的取法m=9,记事件A“所取2人中至少有1人来自第四组”,则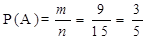 12分
12分
考点:1.数据统计;2.随机事件的概率.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
某次有1000人参加的数学摸底考试,其成绩的频率分布直方图如图所示,规定85分及其以上为优秀.
(1)下表是这次考试成绩的频数分布表,求正整数a, b的值;
| 区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 人数 | 50 | a | 350 | 300 | b |
(3)在(2)中抽取的40名学生中,要随机选取2名学生参 加座谈会,记“其中成绩为优秀的人数”为X,求X的分布列与数学期望.
某年青教师近五年内所带班级的数学平均成绩统计数据如下:
年份 年 年 | 2009 | 2010 | 2011 | 2012 | 2013 |
平均成绩 分 分 | 97 | 98 | 103 | 108 | 109 |
 ,并判断它们之间是正相关还是负相关。
,并判断它们之间是正相关还是负相关。(2)利用(1)中所求出的直线方程预测该教师2014年所带班级的数学平均成绩.

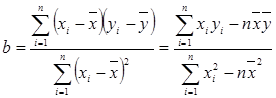






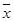 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的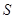 大小为多少?并说明
大小为多少?并说明


 之间的矩形的高,并完成直方图;
之间的矩形的高,并完成直方图; 之间任取两份进行分析,在抽取的结果中,求至少有一份分数在
之间任取两份进行分析,在抽取的结果中,求至少有一份分数在 之间的概率.
之间的概率.
 其中
其中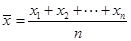
 人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图: ,求
,求 .
.
