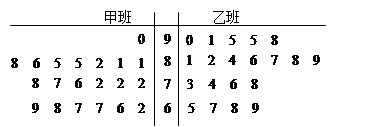题目内容
在每年的春节后,某市政府都会发动公务员参与到植树活动中去.为保证树苗的质量,该市林管部门在植树前,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出树苗的高度如下(单位:厘米):
甲:
乙:
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的10株甲种树苗高度平均值为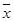 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的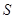 大小为多少?并说明
大小为多少?并说明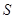 的统计学意义.
的统计学意义.
(1)茎叶图:
统计结论:
①.甲种树苗的平均高度小于乙种树苗的平均高度;
②.甲种树苗比乙种树苗长得更整齐;
③.甲种树苗的中位数为 ,乙种树苗的中位数为
,乙种树苗的中位数为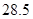 ;
;
④.甲种树苗的高度基本上是对称的,而且大多数集中在均值附近,乙种树苗的高度分布较为分散.
(在以上结论中,写两个即可)
(2) ,
,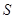 表示
表示 株甲树苗高度的方差,是描述树苗高度离散程度的量.
株甲树苗高度的方差,是描述树苗高度离散程度的量.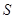 值越小,表示长得越整齐,
值越小,表示长得越整齐,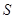 值越大,表示长得越参差不齐.
值越大,表示长得越参差不齐.
解析试题分析:(1)本题中,茎叶图的茎表示十位上的数字(题中已给出),叶表示个位上的数字,故将甲乙两种树苗的高度的个位数字填在两边相应位置上.统计结论从平均数、方差、中位数、众数入手,分析树苗的平均高度及集中度.
(Ⅱ)从框图可以看出,该程序是求树苗高度的方差,所以首先求出甲树苗的高度的平均值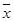 ,然后求出方差
,然后求出方差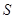 .
.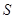 是描述树苗高度离散程度的量.
是描述树苗高度离散程度的量.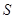 值越小,表示长得越整齐,
值越小,表示长得越整齐,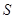 值越大,表示长得越参差不齐.
值越大,表示长得越参差不齐.
试题解析:(1)茎叶图:
统计结论:
①.甲种树苗的平均高度小于乙种树苗的平均高度;
②.甲种树苗比乙种树苗长得更整齐;
③.甲种树苗的中位数为 ,乙种树苗的中位数为
,乙种树苗的中位数为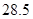 ;
;
④.甲种树苗的高度基本上是对称的,而且大多数集中在均值附近,乙种树苗的高度分布较为分散.
(在以上结论中,每个结论2分,但总分不超过4分)
(2)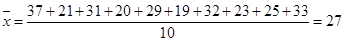 8分
8分 10分
10分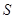 表示
表示 株甲树苗高度的方差,是描述树苗高度离散程度的量.
株甲树苗高度的方差,是描述树苗高度离散程度的量.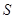 值越小,表示长得越整齐,
值越小,表示长得越整齐,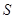 值越大,表示长得越参差不齐. 12分
值越大,表示长得越参差不齐. 12分
考点:统计及样本数据的基本数字特征.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案某高校从今年参加自主招生考试的学生中随机抽取容量为 的学生成绩样本,得到频率分布表如下:
的学生成绩样本,得到频率分布表如下:
| 组数 | 分组 | 频数 | 频率 |
| 第一组 | [230,235) | 8 | 0.16 |
| 第二组 | [235,240) |  | 0.24 |
| 第三组 | [240,245) | 15 |  |
| 第四组 | [245,250) | 10 | 0.20 |
| 第五组 | [250,255] | 5 | 0.10 |
| 合计 |  | 1.00 | |
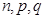 的值;
的值;(2)为了选拔出更加优秀的学生,该高校决定在第三、四、五组中用分层抽样的方法抽取6名学生进行第二轮考核,分别求第三、四、五组参加考核的人数;
(3)在(2)的前提下,高校决定从这6名学生中择优录取2名学生,求2人中至少有1人是第四组的概率.
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
| 年份(x) | 1 | 2 | 3 | 4 | 5 |
| 人数(y) | 3 | 5 | 8 | 11 | 13 |
 年多于10人的概率.
年多于10人的概率.(2)根据这
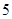 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于 的回归方程
的回归方程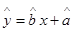 ,并计算第
,并计算第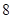 年的估计值。
年的估计值。参考:用最小二乘法求线性回归方程系数公式
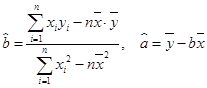
电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名。右图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图。将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性。
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料判断你是否有95%以上的把握认为“体育迷”与性别有关?
| | 非体育迷 | 体育迷 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | |


 的人群随机抽取
的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:

 的值;
的值; 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在 的概率.
的概率.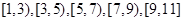 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
 的值及参加“掷铅球”项目测试的人数;
的值及参加“掷铅球”项目测试的人数;
 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求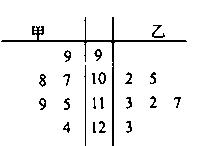
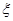 ,试求
,试求