题目内容
某次有1000人参加的数学摸底考试,其成绩的频率分布直方图如图所示,规定85分及其以上为优秀.
(1)下表是这次考试成绩的频数分布表,求正整数a, b的值;
| 区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 人数 | 50 | a | 350 | 300 | b |
(3)在(2)中抽取的40名学生中,要随机选取2名学生参 加座谈会,记“其中成绩为优秀的人数”为X,求X的分布列与数学期望.
(1)  ;(2)30人;(3)分布列
;(2)30人;(3)分布列X 0 1 2 P 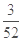
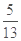
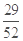
期望为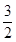 .
.
解析试题分析:(1) 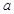 为成绩在
为成绩在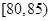 的人数,
的人数,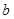 为成绩在
为成绩在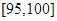 的人数,频率分布直方图中每个小矩形的面积代表样本数据在该区间上的频率,有1000人参加的数学摸底考试,故落在某一区间的人数为该区间的矩形面积乘以总人数.
的人数,频率分布直方图中每个小矩形的面积代表样本数据在该区间上的频率,有1000人参加的数学摸底考试,故落在某一区间的人数为该区间的矩形面积乘以总人数.
(2)分层抽样是按一定比例抽取,但每个个体被抽到的概率相等,所以 .
.
(3) 随机选取2名学生,则2名学生成绩为优秀的人数为0、1、2,利用古典概型分别求出X取值时的概率,写出分布列,利用期望公式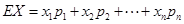 可求期望.
可求期望.
试题解析:(1)依题意,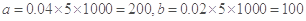 .
.
(2)设其中成绩为优秀的学生人数为x,则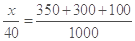 ,解得:x=30,
,解得:x=30,
即其中成绩为优秀的学生人数为30名.
(3)依题意,X的取值为0,1,2,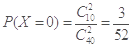 ,
,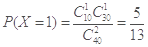 ,
,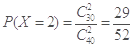 ,
,
所以X的分布列为X 0 1 2 P 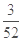
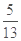
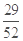
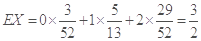 ,所以X的数学期望为
,所以X的数学期望为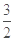 .
.
考点:1、频率分布直方图;2、分层抽样;3、随机事件求概率,数学期望.

练习册系列答案
相关题目
某高校从今年参加自主招生考试的学生中随机抽取容量为 的学生成绩样本,得到频率分布表如下:
的学生成绩样本,得到频率分布表如下:
| 组数 | 分组 | 频数 | 频率 |
| 第一组 | [230,235) | 8 | 0.16 |
| 第二组 | [235,240) |  | 0.24 |
| 第三组 | [240,245) | 15 |  |
| 第四组 | [245,250) | 10 | 0.20 |
| 第五组 | [250,255] | 5 | 0.10 |
| 合计 |  | 1.00 | |
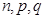 的值;
的值;(2)为了选拔出更加优秀的学生,该高校决定在第三、四、五组中用分层抽样的方法抽取6名学生进行第二轮考核,分别求第三、四、五组参加考核的人数;
(3)在(2)的前提下,高校决定从这6名学生中择优录取2名学生,求2人中至少有1人是第四组的概率.


 ,求
,求 .
. 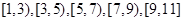 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
 的值及参加“掷铅球”项目测试的人数;
的值及参加“掷铅球”项目测试的人数; 人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
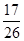 ,求
,求 的值;
的值;
 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求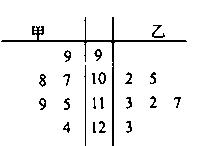
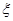 ,试求
,试求 ,(单位:元).
,(单位:元).
 的概率;
的概率;