题目内容
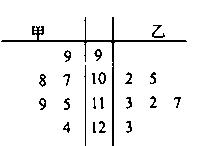
某中学高三年级从甲、乙两个班级各选出七名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,
(1)求x和y的值;
(2)计算甲班七名学生成绩的方差;
(3)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
参考公式:方差 其中
其中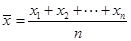
(1)x=5,y=3;(2)40;(3)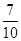
解析试题分析:(1)根据平均数计算公式可求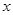 ,中位数是指将一组数据按照从小到大或者从大到小的顺序排成一列,如果是奇数个数,中位数是最中间的数;如果是偶数个数,中位数是最中间两个数的平均数,由题知
,中位数是指将一组数据按照从小到大或者从大到小的顺序排成一列,如果是奇数个数,中位数是最中间的数;如果是偶数个数,中位数是最中间两个数的平均数,由题知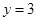 ;(2)甲班七名学生成绩已知,代入方差计算公式即可;(3)记事件
;(2)甲班七名学生成绩已知,代入方差计算公式即可;(3)记事件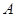 =“从中抽取两名学生,甲班至少有一名学生”,把成绩在90分以上的学生编号,列出从中抽取两名学生的基本事件总数以及事件
=“从中抽取两名学生,甲班至少有一名学生”,把成绩在90分以上的学生编号,列出从中抽取两名学生的基本事件总数以及事件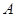 包含的基本事件总数,代入古典概型的概率计算公式可求;至少、至多问题的概率还可以根据对立事件的概率来求,即
包含的基本事件总数,代入古典概型的概率计算公式可求;至少、至多问题的概率还可以根据对立事件的概率来求,即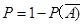 .
.
试题解析:(1)由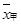 =85,得
=85,得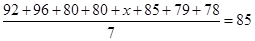 ,所以
,所以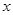 =5,将数字按照从小到大的顺序排列,第四个数字是中位数,所以
=5,将数字按照从小到大的顺序排列,第四个数字是中位数,所以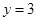 ;
;
(2)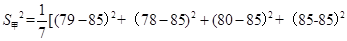
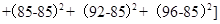 =40;
=40;
(3)成绩在90分以上的学生共有5名,其中甲班有两名,记为a,b,乙班3名,记为1,2,3,从中任取两名,基本事件为有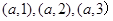 ,
,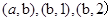 ,
,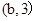 ,
,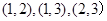 ,共10个,记事件
,共10个,记事件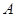 =“从中抽取两名学生,甲班至少有一名学生”,则事件
=“从中抽取两名学生,甲班至少有一名学生”,则事件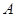 包含的基本事件有
包含的基本事件有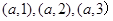 ,
,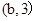 ,
,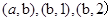 ,共7个,所以
,共7个,所以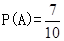 .
.
考点:1、茎叶图;2、平均数、方差和中位数;3、古典概型.

某高校从今年参加自主招生考试的学生中随机抽取容量为 的学生成绩样本,得到频率分布表如下:
的学生成绩样本,得到频率分布表如下:
| 组数 | 分组 | 频数 | 频率 |
| 第一组 | [230,235) | 8 | 0.16 |
| 第二组 | [235,240) |  | 0.24 |
| 第三组 | [240,245) | 15 |  |
| 第四组 | [245,250) | 10 | 0.20 |
| 第五组 | [250,255] | 5 | 0.10 |
| 合计 |  | 1.00 | |
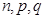 的值;
的值;(2)为了选拔出更加优秀的学生,该高校决定在第三、四、五组中用分层抽样的方法抽取6名学生进行第二轮考核,分别求第三、四、五组参加考核的人数;
(3)在(2)的前提下,高校决定从这6名学生中择优录取2名学生,求2人中至少有1人是第四组的概率.
电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名。右图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图。将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性。
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料判断你是否有95%以上的把握认为“体育迷”与性别有关?
| | 非体育迷 | 体育迷 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | |


某年某省有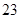 万多文科考生参加高考,除去成绩为
万多文科考生参加高考,除去成绩为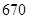 分(含
分(含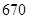 分)以上的
分)以上的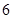 人与成绩为
人与成绩为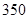 分(不含
分(不含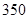 分)以下的
分)以下的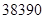 人,还有约
人,还有约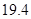 万文科考生的成绩集中在
万文科考生的成绩集中在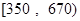 内,其成绩的频率分布如下表所示:
内,其成绩的频率分布如下表所示:
| 分数段 | 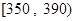 | 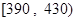 | 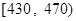 | 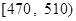 |
| 频率 | 0.108 | 0.133 | 0.161 | 0.183 |
| 分数段 | 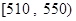 | 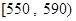 | 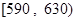 | 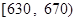 |
| 频率 | 0.193 | 0.154 | 0.061 | 0.007 |
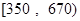 内文科考生的平均分(精确到
内文科考生的平均分(精确到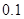 );
);(2)考生A填报志愿后,得知另外有4名同分数考生也填报了该志愿.若该志愿计划录取2人,并在同分数考生中随机录取,求考生A被该志愿录取的概率.
(参考数据:610×0.061+570×0.154+530×0.193+490×0.183+450×0.161+410×0.133=443.93)

 ,求
,求 .
. 
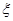 ,试求
,试求
 ,(单位:元).
,(单位:元).
 的概率;
的概率; 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题: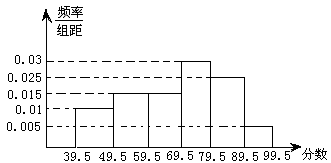
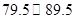 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?