题目内容
【题目】已知函数(x)=xlnx,g(x)=ax3-![]() .
.
(Ⅰ)求函数(x)的单调递增区间和最小值;
(Ⅱ)若函数y= (x)与函数y =g(x)的图象在交点处存在公共切线,求实数a的值。
【答案】(Ⅰ) 见解析;(Ⅱ)a=![]() .
.
【解析】试题分析:(Ⅰ)求出![]() 的导数,求得单调区间和极值,即可得最小值;(Ⅱ)设函数
的导数,求得单调区间和极值,即可得最小值;(Ⅱ)设函数![]() 与函数
与函数![]() 的图象在交点
的图象在交点![]() 处存在公共切线,则根据切线的斜率相等以及交点在两个函数的图象上可得
处存在公共切线,则根据切线的斜率相等以及交点在两个函数的图象上可得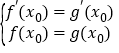 ,列出方程组,结合(Ⅰ),即可求出实数
,列出方程组,结合(Ⅰ),即可求出实数![]() 的值.
的值.
试题解析:(Ⅰ)∵![]()
∴![]() ,
,![]()
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
∴所求函数![]() 的单调递增区间为
的单调递增区间为![]() ,最小值为
,最小值为![]() .
.
(Ⅱ) 设函数![]() 与函数
与函数![]() 的图象在交点
的图象在交点![]() 处存在公共切线,则根据切线的斜率相等以及交点在两个函数的图象上可得
处存在公共切线,则根据切线的斜率相等以及交点在两个函数的图象上可得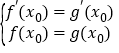 , 即
, 即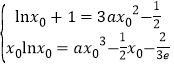 (*),变形得
(*),变形得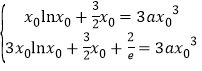 .
.
∴![]() ,化简得
,化简得![]()
∴![]() 是方程
是方程![]() 的一个实数解.
的一个实数解.
又∵由(Ⅰ)易知方程![]() 有唯一的实数解,且该解为
有唯一的实数解,且该解为![]()
∴![]() ,将之代入
,将之代入![]()
∴![]()

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目