题目内容
【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:min)的频率分布直方图,若将日均课外阅读时间不低于60 min的学生称为“书虫”,低于60 min的学生称为“懒虫”,

(1)求x的值并估计全校3 000名学生中“书虫”大概有多少名学生?(将频率视为概率)
(2)根据已知条件完成下面2×2的列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“书虫”与性别有关:

【答案】(1)x=0.025,1200人;(2)见解析.
【解析】试题分析:(1)由直方图,易知x=0.025,“书虫”大概有1200人;(2)完成表格,K2=≈8.249.由8.249>6.635,故在犯错误的概率不超过0.01的前提下认为“读书迷”与性别有关.
试题解析:
(1)由已知可得:(0.01+0.02+0.03+x+0.015)×10=1,可得x=0.025
因为(0.025+0.015)×10=0. 4,将频率视为概率,由此可以估算出全校3000名学生中“书虫”大概有1200人.
(2)完成下面的2×2列联表如下:
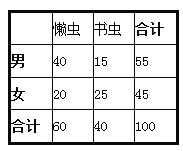
K2=≈8.249.
由8.249>6.635,故在犯错误的概率不超过0.01的前提下认为“读书迷”与性别有关.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目