题目内容
如图1,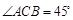 ,
,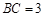 ,过动点A作
,过动点A作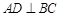 ,垂足
,垂足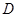 在线段
在线段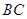 上且异于点
上且异于点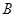 ,连接
,连接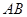 ,沿
,沿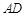 将△
将△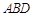 折起,使
折起,使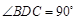 (如图2所示).
(如图2所示).

(1)当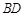 的长为多少时,三棱锥
的长为多少时,三棱锥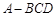 的体积最大;
的体积最大;
(2)当三棱锥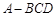 的体积最大时,设点
的体积最大时,设点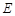 ,
,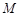 分别为棱
分别为棱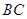 、
、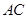 的中点,试在棱
的中点,试在棱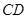 上确定一点
上确定一点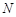 ,使得
,使得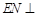
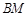 ,并求
,并求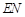 与平面
与平面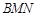 所成角的大小.
所成角的大小.
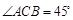 ,
,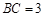 ,过动点A作
,过动点A作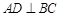 ,垂足
,垂足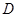 在线段
在线段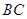 上且异于点
上且异于点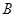 ,连接
,连接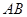 ,沿
,沿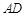 将△
将△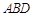 折起,使
折起,使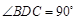 (如图2所示).
(如图2所示). 
(1)当
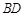 的长为多少时,三棱锥
的长为多少时,三棱锥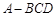 的体积最大;
的体积最大;(2)当三棱锥
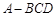 的体积最大时,设点
的体积最大时,设点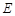 ,
,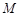 分别为棱
分别为棱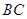 、
、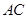 的中点,试在棱
的中点,试在棱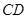 上确定一点
上确定一点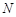 ,使得
,使得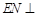
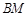 ,并求
,并求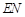 与平面
与平面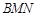 所成角的大小.
所成角的大小.(1) 时, 三棱锥
时, 三棱锥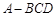 的体积最大.(2)
的体积最大.(2)
 时, 三棱锥
时, 三棱锥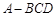 的体积最大.(2)
的体积最大.(2)
试题分析:(1)解法1:在如图1所示的△
 中,设
中,设 ,则
,则 .
.由
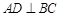 ,
,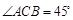 知,△
知,△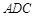 为等腰直角三角形,所以
为等腰直角三角形,所以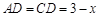 .
.由折起前
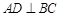 知,折起后(如图2),
知,折起后(如图2),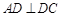 ,
, ,且
,且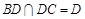 ,
,所以
 平面
平面 .又
.又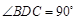 ,所以
,所以 .于是
.于是
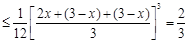 ,
,当且仅当
 ,即
,即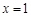 时,等号成立
时,等号成立 故当
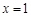 ,即
,即 时, 三棱锥
时, 三棱锥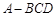 的体积最大.
的体积最大. 解法2:同解法1,得
 .
. 令
 ,由
,由 ,且
,且 ,解得
,解得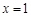 .
.当
 时,
时, ;当
;当 时,
时, .
. 所以当
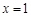 时,
时, 取得最大值.
取得最大值.故当
 时, 三棱锥
时, 三棱锥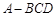 的体积最大.
的体积最大.(2)解法1:以D为原点,建立如图a所示的空间直角坐标系D-
 .
.由(Ⅰ)知,当三棱锥A-BCD的体积最大时,BD=1,AD=CD=2.
于是可得D(0,0,0,),B(1,0,0),C(0,2,0),A(0,0,2)M(0,1,1)E(
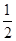 ,1,0),且BM=(-1,1,1).
,1,0),且BM=(-1,1,1). 设N(0,
 , 0),则EN=
, 0),则EN= ,
, -1,0).因为EN⊥BM等价于EN·BM=0,即(
-1,0).因为EN⊥BM等价于EN·BM=0,即( ,
, -1,0)·(-1,1,1)=
-1,0)·(-1,1,1)=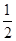 +
+ -1=0,故
-1=0,故 =
=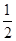 ,N(0,
,N(0, 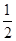 ,0)
,0) 所以当DN=
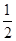 时(即N是CD的靠近点D的一个四等分点)时,EN⊥BM.
时(即N是CD的靠近点D的一个四等分点)时,EN⊥BM.设平面BMN的一个法向量为n=(
 ,
,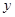 ,
,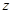 ),由
),由 可取
可取 =(1,2,-1)
=(1,2,-1) 设
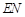 与平面
与平面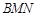 所成角的大小为
所成角的大小为 ,则由
,则由 ,
, ,可得
,可得
 ,即
,即 .
. 故
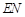 与平面
与平面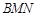 所成角的大小为
所成角的大小为
解法2:由(Ⅰ)知,当三棱锥
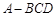 的体积最大时,
的体积最大时, ,
, .
.如图b,取
 的中点
的中点 ,连结
,连结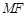 ,
,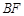 ,
, ,则
,则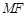 ∥
∥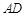 .
.由(Ⅰ)知
 平面
平面 ,所以
,所以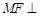 平面
平面 .
.如图c,延长
 至P点使得
至P点使得 ,连
,连 ,
, ,则四边形
,则四边形 为正方形,
为正方形,所以
 . 取
. 取 的中点
的中点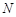 ,连结
,连结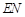 ,又
,又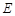 为
为 的中点,则
的中点,则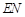 ∥
∥ ,
,所以
 . 因为
. 因为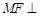 平面
平面 ,又
,又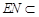 面
面 ,所以
,所以 .
. 又
 ,所以
,所以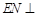 面
面 . 又
. 又 面
面 ,所以
,所以 .
.因为
 当且仅当
当且仅当 ,而点F是唯一的,所以点
,而点F是唯一的,所以点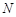 是唯一的.
是唯一的.即当
 (即
(即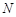 是
是 的靠近点
的靠近点 的一个四等分点),
的一个四等分点), .
. 连接
 ,
, ,由计算得
,由计算得 ,
,所以△
 与△
与△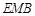 是两个共底边的全等的等腰三角形,
是两个共底边的全等的等腰三角形,如图d所示,取
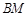 的中点
的中点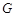 ,连接
,连接 ,
, ,
,则
 平面
平面 .在平面
.在平面 中,过点
中,过点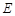 作
作 于
于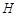 ,
,则
 平面
平面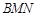 .故
.故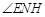 是
是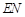 与平面
与平面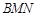 所成的角.
所成的角. 在△
 中,易得
中,易得 ,所以△
,所以△ 是正三角形,
是正三角形,故
 ,即
,即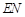 与平面
与平面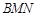 所成角的大小为
所成角的大小为
点评:本题主要考查了线面垂直的判定,折叠问题中的不变量,空间线面角的计算方法,空间向量、空间直角坐标系的运用,有一定的运算量,属中档题

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
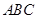 中,
中, ,
, ,
, 分别是
分别是 上的点,
上的点, ,
, 为
为 的中点.将
的中点.将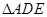 沿
沿 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥 ,其中
,其中 .
.
 平面
平面 ;
; 的平面角的余弦值.
的平面角的余弦值.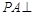 平面ABCD,
平面ABCD,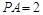 ,E是PC上的一点.
,E是PC上的一点.
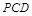 ;
;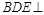 平面
平面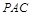 ;
;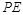 为多长时,
为多长时,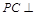 平面
平面 ?
?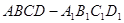 中,面
中,面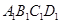 中心为
中心为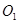 .
.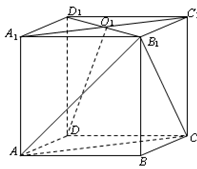
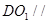 面
面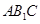 ;
;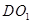 与
与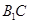 所成角.
所成角.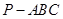 中,
中,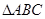 是底面,
是底面,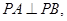
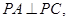
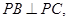 且这四个顶点都在半径为2的球面上,
且这四个顶点都在半径为2的球面上,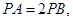 则这个三棱锥的三个侧棱长的和的最大值为( )
则这个三棱锥的三个侧棱长的和的最大值为( )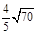
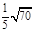
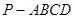 的底面是正方形,侧棱与底面边长均为2,则其侧视图的面积为_____.
的底面是正方形,侧棱与底面边长均为2,则其侧视图的面积为_____.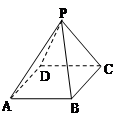
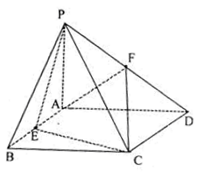
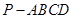 中,
中,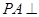 平面
平面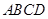 ,四边形
,四边形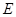 ,
,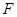 分别是
分别是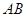 ,
,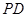 的中点.若
的中点.若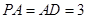 ,
,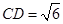 。
。
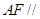 平面
平面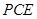 ;
;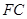 平面
平面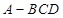 中,侧棱
中,侧棱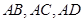 两两垂直,
两两垂直,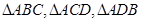 的
的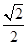 、
、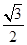 、
、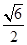 .则三棱锥
.则三棱锥