题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{x+\frac{4}{x}(x>0)}\\{{x}^{3}+4(x≤0)}\end{array}\right.$,若关于x的方程f(x2)=a(a∈R)有四个不同的实根,则a的取值范围是( )| A. | (4,+∞) | B. | [4,+∞) | C. | (-∞,4) | D. | (4,7) |
分析 令t=x2,则t≥0,函数f(t)=$\left\{\begin{array}{l}{t+\frac{4}{t},t>0}\\{{t}^{3}+4,t≤0}\end{array}\right.$,由题意可得,函数f(t)的图象与直线y=a有4个不同的交点,且每个t值有2个x值与之对应,数形结合可得a的取值范围.
解答 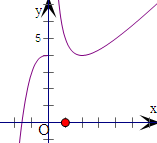 解:令t=x2,则t≥0,
解:令t=x2,则t≥0,
函数f(t)=$\left\{\begin{array}{l}{t+\frac{4}{t},t>0}\\{{t}^{3}+4,t≤0}\end{array}\right.$.
由题意可得,函数f(t)的图象与直线y=a有2个不同的交点,
且每个t值有2个x值与之对应,如图所示:
由于当t=2时,f(t)=4,
当a>4时,有两个t值,即有4个不同的实根.
故选A.
点评 本题主要考查函数的零点与方程的根的关系,体现了数形结合的数学思想及等价转化的数学思想,属于中档题.

练习册系列答案
相关题目
18.曲线y=ax2-ax+1(a≠0)在点(0,1)处的切线与直线3x+y+1=0垂直,则a=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
16.已知F为抛物线y2=x的焦点,点A、B在该抛物线上且位于x轴两侧,$\overrightarrow{OA}$$•\overrightarrow{OB}$=6(O为坐标原点),则△ABO与△AOF面积之和的最小值为( )
| A. | 4 | B. | $\frac{3\sqrt{13}}{2}$ | C. | $\frac{17\sqrt{2}}{4}$ | D. | $\sqrt{10}$ |