题目内容
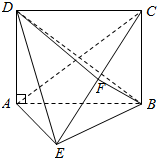
20．已知正方形ABCD的边长为8，空间有一点M（不在平面ABCD内）满足|MA|+|MB|=10，则三棱锥M-ABC的体积的最大值是32．分析 由已知点M（不在平面ABCD内）满足|MA|+|MB|=10，可得点M在以A，B为焦点的椭球上（去掉在平面ABCD内的点），球心为O．当MO⊥平面ABCD时，MO=$\sqrt{A{M}^{2}-A{O}^{2}}$，此时三棱锥的高最大，即可得出．
解答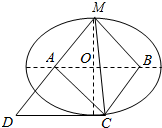 
解：由已知点M（不在平面ABCD内）满足|MA|+|MB|=10，可得点M在以A，B为焦点的椭球上（去掉在平面ABCD内的点），球心为O．
当MO⊥平面ABCD时，MO=$\sqrt{A{M}^{2}-A{O}^{2}}$=3，此时三棱锥的高最大，
因此三棱锥A-BCM的体积的最大值=$\frac{1}{3}•MO•{S}_{△ABC}$=$\frac{1}{3}×3×\frac{1}{2}×{8}^{2}$=32．
故答案为：32．
点评 本题考查了椭球的定义及其性质、线面面面垂直的性质、三棱锥的体积计算公式、勾股定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
11．已知角α，β均为锐角，且tanα=$\frac{4}{3}，tan（α-β）=-\frac{1}{3}$，则tanβ=（ ）
| A． | $\frac{1}{3}$ | B． | 3 | C． | $\frac{13}{9}$ | D． | $\frac{9}{13}$ |
8．已知函数f（x）=$\left\{\begin{array}{l}{x+\frac{4}{x}（x＞0）}\\{{x}^{3}+4（x≤0）}\end{array}\right.$，若关于x的方程f（x2）=a（a∈R）有四个不同的实根，则a的取值范围是（ ）
| A． | （4，+∞） | B． | [4，+∞） | C． | （-∞，4） | D． | （4，7） |
5．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1、F2，离心率为$\frac{\sqrt{3}}{3}$，过F2的直线l交C于A、B两点，若△AF1B的周长为12，则C的方程为（ ）
| A． | $\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1 | B． | $\frac{{x}^{2}}{3}$+y2=1 | C． | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | D． | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{6}$=1 |
