题目内容
16.已知F为抛物线y2=x的焦点,点A、B在该抛物线上且位于x轴两侧,$\overrightarrow{OA}$$•\overrightarrow{OB}$=6(O为坐标原点),则△ABO与△AOF面积之和的最小值为( )| A. | 4 | B. | $\frac{3\sqrt{13}}{2}$ | C. | $\frac{17\sqrt{2}}{4}$ | D. | $\sqrt{10}$ |
分析 先设直线方程和点的坐标,联立直线与抛物线的方程得到一个一元二次方程,再利用韦达定理及$\overrightarrow{OA}$$•\overrightarrow{OB}$=6消元,最后将面积之和表示出来,探求最值问题.
解答 解:设直线AB的方程为:x=ty+m,
点A(x1,y1),B(x2,y2),
直线AB与x轴的交点为M(m,0),
x=ty+m代入y2=x,可得y2-ty-m=0,
根据韦达定理有y1•y2=-m,
∵$\overrightarrow{OA}$$•\overrightarrow{OB}$=6,
∴x1•x2+y1•y2=6,从而(y1•y2)2+y1•y2-6=0,
∵点A,B位于x轴的两侧,
∴y1•y2=-3,故m=3.
不妨令点A在x轴上方,则y1>0,
又F($\frac{1}{4}$,0),
∴S△ABO+S△AFO=$\frac{1}{2}$×3×(y1-y2)+$\frac{1}{2}$×$\frac{1}{4}$y1=$\frac{13}{8}$y1+$\frac{9}{2{y}_{1}}$
≥2$\sqrt{\frac{9×13}{16}}$=$\frac{3\sqrt{13}}{2}$,
当且仅当$\frac{13}{8}$y1=$\frac{9}{2{y}_{1}}$,即y1=$\frac{6\sqrt{13}}{13}$时,取“=”号,
∴△ABO与△AFO面积之和的最小值是$\frac{3\sqrt{13}}{2}$,
故选:.
点评 求解本题时,应考虑以下几个要点:
1、联立直线与抛物线的方程,消x或y后建立一元二次方程,利用韦达定理与已知条件消元,这是处理此类问题的常见模式.
2、求三角形面积时,为使面积的表达式简单,常根据图形的特征选择适当的底与高.
3、利用基本不等式时,应注意“一正,二定,三相等”.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案| A. | 2k+1 | B. | 2k+2 | C. | (2k+1)+(2k+2) | D. | (k+1)+(k+2)+…+2k |
| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{13}{9}$ | D. | $\frac{9}{13}$ |
| A. | (4,+∞) | B. | [4,+∞) | C. | (-∞,4) | D. | (4,7) |
| A. | $\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{3}$+y2=1 | C. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{6}$=1 |
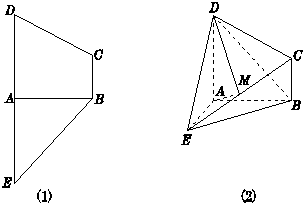 如图所示,在梯形BCDE中,BC∥DE,BA⊥DE,且EA=DA=AB=2CB=2,沿AB将四边形ABCD折起,使得平面ABCD与平面ABE垂直,M为CE的中点.
如图所示,在梯形BCDE中,BC∥DE,BA⊥DE,且EA=DA=AB=2CB=2,沿AB将四边形ABCD折起,使得平面ABCD与平面ABE垂直,M为CE的中点.