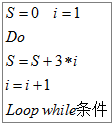��Ŀ����
3����Ȳ�����{an}��ǰn���ΪSn����a2+a16=34��S4=16������{bn}��ǰn���ΪTn������Tn+bn=1����1��������{an}��ͨ�ʽ��
��2��д��һ��������m��ʹ��$\frac{1}{{{a_m}+9}}$������{bn}���
��3��������{cn}��ͨ�ʽΪcn=$\frac{a_n}{{{a_n}+t}}$���ʣ��Ƿ����������t��k��k��3����ʹ��c1��c2��ck�ɵȲ����У������ڣ���������з������������������ԣ�t��k�����������ڣ���˵�����ɣ�
���� ��1��ͨ���ⷽ����$\left\{\begin{array}{l}{2{a}_{1}+16d=34}\\{4{a}_{1}+6d=16}\end{array}\right.$����������ɵý��ۣ�
��2��ͨ��Tn=1-bn��Tn+1=1-bn+1�����֪����{bn}��������Ⱦ�Ϊ$\frac{1}{2}$�ĵȱ����У�ͨ������ֻҪm+42n���ɣ�
��3��ͨ����1��֪cn=$\frac{2n-1}{2n-1+t}$������ֻ��k=3+$\frac{4}{t-1}$�����ǵ�k��t����������������ѡȡ�����鼴�ɣ�
��� �⣺��1��������{an}������Ϊa1������Ϊd��
����֪����$\left\{\begin{array}{l}{2{a}_{1}+16d=34}\\{4{a}_{1}+6d=16}\end{array}\right.$��
��ã�a1=1��d=2��
������{an}��ͨ�ʽan=2n-1��
��2����n=1ʱ��b1=T1=1-b1������b1=$\frac{1}{2}$��
��Tn=1-bn����Tn+1=1-bn+1��
��ʽ������ã�bn+1=bn-bn+1����bn+1=$\frac{1}{2}$bn��
������{bn}��������Ⱦ�Ϊ$\frac{1}{2}$�ĵȱ����У�
��bn=$\frac{1}{{2}^{n}}$��
��$\frac{1}{{a}_{m}+9}$=$\frac{1}{2m+8}$=$\frac{1}{2��m+4��}$��
��Ҫʹ$\frac{1}{{a}_{m}+9}$������{bn}�е��ֻҪm+4=2n���ɣ�
�ʿ�ȡm=4��
��3�����ۣ����ڷ���������������t��k�����з������������������ԣ�t��k��Ϊ����2��7������3��5������5��4����
�������£�
�ɣ�1��֪��cn=$\frac{2n-1}{2n-1+t}$��
Ҫʹc1��c2��ck�ɵȲ����У�����2c2=c1+ck��
��$\frac{6}{3+t}$=$\frac{1}{1+t}$+$\frac{2k-1}{2k-1+t}$�������k=3+$\frac{4}{t-1}$��
��Ϊk��t����������������tֻ��ȡ2��3��5��
��t=2ʱ��k=7��
��t=3ʱ��k=5��
��t=5ʱ��k=4��
���Ͽ�֪�����ڷ���������������t��k��
���з������������������ԣ�t��k��Ϊ����2��7������3��5������5��4����
���� ���⿼�����е�ͨ�ע����ⷽ���Ļ��ۣ������е��⣮

 ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 90�� |
| A�� | $\frac{1}{3}$ | B�� | 3 | C�� | $\frac{13}{9}$ | D�� | $\frac{9}{13}$ |
| A�� | ��4��+�ޣ� | B�� | [4��+�ޣ� | C�� | ��-�ޣ�4�� | D�� | ��4��7�� |
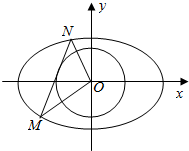 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���ϵĵ㵽������ľ����Ϊ$\frac{2}{3}$�����᳤Ϊ$\frac{1}{2}$��ֱ��l����ԲC����M��N���㣮
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���ϵĵ㵽������ľ����Ϊ$\frac{2}{3}$�����᳤Ϊ$\frac{1}{2}$��ֱ��l����ԲC����M��N���㣮