已知数列a0=1.an=nan-1+1.用框图和语句表示算法.输出使an≤50的最大的正整数n．题目和参考答案——青夏教育精英家教网——

题目内容

13．已知数列a₀=1，a_n=na_n-1+1，用框图和语句表示算法，输出使a_n≤50的最大的正整数n．

分析由题目给出的数列递推式，利用循环结构得程序框图，结合算法及框图写出相应程序语句即可．

解答解：程序框图如下：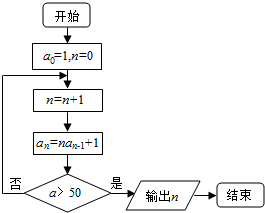

语句如下：
a₀=1
Do n=0
n=n+1
a_n=na_n-1+1
Loop While a≤50
输出n

点评本题考查了设计程序框图解决实际问题，由数列的递推公式求解数列的通项公式，属于基础题．

练习册系列答案

期末夺冠卷系列答案

期末轻松100分系列答案

期末考试卷系列答案

北斗星期末大冲刺系列答案

全能测试卷系列答案

快乐5加2金卷系列答案

阶段性单元目标大试卷系列答案

金版卷王名师面对面大考卷系列答案

复习与考试系列答案

单元测试AB卷光明日报出版社系列答案

相关题目

3．函数$f（x）={（{\frac{1}{2}}）^{lg（{x^2}-2x-3）}}$的定义域为（-∞，-1）∪（3，+∞），单调递减区间是（3，+∞）．

4．若θ∈（0°，360°）且终边与660°角的终边关于x轴对称，点P（x，y）在θ角的终边上（不是原点），求$\frac{xy}{{x}^{2}+{y}^{2}}$的值．

1．已知函数f（x）=$\sqrt{3}$sin（2x-$\frac{π}{6}$）+2sin²（x-$\frac{π}{12}$）（x∈R）．
（1）求函数f（x）的最小正周期；
（2）求f（x）的单调增区间；
（3）若x∈[0，2π]时，求函数f（x）的零点．

8．已知函数f（x）=$\left\{\begin{array}{l}{x+\frac{4}{x}（x＞0）}\\{{x}^{3}+4（x≤0）}\end{array}\right.$，若关于x的方程f（x²）=a（a∈R）有四个不同的实根，则a的取值范围是（　　）

18．有一天猎手带着他的两头猎犬跟踪某动物的踪迹，他们来达到一个三岔口，现在需要从两个方向中选择一个追踪方向，猎手知道两条猎犬会相互独立地以概率p找到正确的方向，因此他让两条猎犬选择它们的方向，如果两头猎犬选择同一方向，他就沿着这个方向走，若两条猎犬选择不同的方向，他就随机地选择一个方向走，这个策略是否比只让一个猎犬选择方向优越？

5．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F₁、F₂，离心率为$\frac{\sqrt{3}}{3}$，过F₂的直线l交C于A、B两点，若△AF₁B的周长为12，则C的方程为（　　）

$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1

$\frac{{x}^{2}}{3}$+y²=1

$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1

$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{6}$=1

2．已知函数$f（x）=2\sqrt{3}sinxcosx+{cos^2}x-{sin^2}x$
（1）求f（x）的最小正周期及单调增区间；
（2）当$x∈[-\frac{π}{6}，\frac{π}{3}]$时，求函数f（x）的值域．

3．已知数列{a_n}，{b_n}中，a₁=a，{b_n}是公比为$\frac{2}{3}$的等比数列．记b_n=$\frac{{a}_{n}-2}{{a}_{n}-1}$（n∈N^*）若不等式a_n＞a_n+1对一切n∈N^*恒成立，则实数a的取值范围是（　　）

（$\frac{3}{2}$，+∞）