题目内容
12.在△ABC中,已知b=2,a=3,cosA=-$\frac{4}{5}$.(1)求sinB;
(2)求sin(2B+$\frac{π}{6}$).
分析 (1)由题意和同角三角函数基本关系可得sinA,由正弦定理可得sinB=$\frac{bsinA}{a}$,代值计算可得;
(2)同理可得cosB,进而由二倍角公式可得sin2B和cos2B,代入sin(2B+$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$sin2B+$\frac{1}{2}$cos2B计算可得.
解答 解:(1)∵在△ABC中b=2,a=3,cosA=-$\frac{4}{5}$,
∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{3}{5}$,
∴由正弦定理可得sinB=$\frac{bsinA}{a}$=$\frac{2×\frac{3}{5}}{3}$=$\frac{2}{5}$;
(2)由(1)知sinB=$\frac{2}{5}$,cosA=-$\frac{4}{5}$<0,
∴A为钝角,B为锐角,
∴cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{\sqrt{21}}{5}$,
∴sin2B=2sinBcosB=$\frac{4\sqrt{21}}{25}$
cos2B=cos2B-sin2B=$\frac{17}{25}$
∴sin(2B+$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$sin2B+$\frac{1}{2}$cos2B
=$\frac{\sqrt{3}}{2}×\frac{4\sqrt{21}}{25}$+$\frac{1}{2}×\frac{17}{25}$=$\frac{12\sqrt{7}+17}{50}$
点评 本题考查解三角形,涉及正弦定理和和差角的三角函数公式以及同角三角函数基本关系,属中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
20.在极坐标系中,曲线C的方程为F(ρ,θ)=0,则F(ρ0,θ0)=0是点P(ρ0,θ0)在曲线C上的( )
| A. | 充要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 非充分非必要条件 |
4.函数f(x)的定义域为R,f(-1)=1,对任意x∈R,f′(x)>2,则f(x)>2x+3的解集为( )
| A. | (-1,1) | B. | (-1,+∞) | C. | (-∞,-1) | D. | (-∞,+∞) |
1.若a>0,b>0,且a+b=2,则ab+$\frac{1}{ab}$的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 2$\sqrt{2}$ |
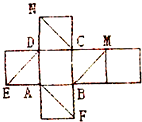 如图是正方体的平面展开图,在这个正方体中:
如图是正方体的平面展开图,在这个正方体中: