如图是正方体的平面展开图.在这个正方体中:①BM与DE平行 ②CN与BE是异面直线③CN与BM成60°角 ④DM与BN垂直以上四个命题中.正确的是( )A．①②③B．②④C．②③④D．③④ 题目和参考答案——青夏教育精英家教网—

题目内容

3．

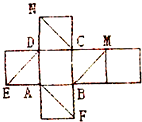如图是正方体的平面展开图，在这个正方体中：
①BM与DE平行 ②CN与BE是异面直线
③CN与BM成60°角 ④DM与BN垂直
以上四个命题中，正确的是（　　）

A．

①②③

B．

②④

C．

②③④

D．

③④

分析如图所示，原正方体为，在这个正方体中：
①BM与DE为异面直线，即可判断出正误；
②CN与BE是平行直线，即可判断出正误；
③由正方体的性质可得△DEM为等边三角形，即可得出CN与BM所成的角；
④由正方体可得：DM⊥平面BCEN，即可判断出正误．

解答解：如图所示，原正方体为：
在这个正方体中：
①BM与DE为异面直线，因此不正确；
②CN与BE是平行直线，因此不正确；
③连接BE，EM，则BE∥CN，△DEM为等边三角形，∴BE与BM成60°角，因此CN与BM成60°角，因此正确；
④由正方体可得：DM⊥平面BCEN，∴DM与BN垂直，正确．
以上四个命题中，正确的是③④．
故选：D．

点评本题考查了正方体的性质、空间角、空间线面位置关系，考查了推理能力与计算能力，属于中档题．

练习册系列答案

14．已知在平面直角坐标系xOy中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞1）的一个焦点为F₁（-$\sqrt{3}$，0），M（1，y）（y＞0）为椭圆上的一点，△MOF₁的面积为$\frac{3}{4}$，求椭圆C的标准方程．

11．已知数列{a_n}的前n项和S_n满足$\frac{1}{2}$S_n=a_n-1．
（1）求数列{a_n}的通项公式；
（2）求证：数列{a_n}中的任意三项不可能成等差数列；
（3）设b_n=$\frac{{a}_{n}}{（{a}_{n}-1）^{2}}$，T_n为{b_n}的前n项和，求证：T_n＜3．

18．下列各项表示同一个函数的是（　　）

	A．	f（x）=$\frac{{x}^{2}-1}{x-1}$与g（x）=x+1		B．	f（x）=$\sqrt{{x}^{2}}$-1与g（x）=x-1
	C．	f（x）=$\frac{（x+3）^{2}}{x+3}$，g（x）=（x+3）（x+3）⁰		D．	f（x）=$\sqrt{-2{x}^{3}}$与g（x）=x$\sqrt{-2x}$

8．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+y²=1（a＞0）的焦点在x轴上，右顶点与上顶点分别为A，B，顶点在原点，分别以A，B为焦点的抛物线C₁，C₂交于点P（不同于O点），且以BP为直径的圆经过点A．
（1）求椭圆C的标准方程．
（2）若与OP垂直的动直线l交椭圆C于M，N不同两点，求△OMN面积的最大值和此时直线l的方程．

15．已知函数f（x）=lnx-mx，m∈R．
（1）若m=1，求曲线y=f（x）在点P（1，-1）处的切线方程；
（2）若f（x）没有零点，求实数m的取值范围．

12．在△ABC中，已知b=2，a=3，cosA=-$\frac{4}{5}$．
（1）求sinB；
（2）求sin（2B+$\frac{π}{6}$）．

13．集合A={x|x²+x+3=0，x∈R}，B={x|x²+2x-15≤0}，则A∪B=[-5，3]．

试题分类