题目内容
【题目】已知椭圆![]() :
: ![]() 的一个焦点
的一个焦点![]() 与抛物线
与抛物线![]() 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为![]() .
.
(1)求该椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且点
两点,且点![]() 恰为弦
恰为弦![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由已知条件求出![]() 的值,得出椭圆的方程;(2)由“点差法”求出直线
的值,得出椭圆的方程;(2)由“点差法”求出直线![]() 的斜率,由直线的点斜式求出直线方程。
的斜率,由直线的点斜式求出直线方程。
试题解析:(1)抛物线y2=4x的焦点为F(1,0),准线方程为x=﹣1,
∴a2﹣b2=1 ①,
又椭圆截抛物线的准线x=﹣1所得弦长为3,
∴可得上面的交点为(﹣1, ![]() ),∴
),∴![]() ②
②
由①代入②得4b4﹣9b2﹣9=0,解得b2=3或b2=![]() (舍去),
(舍去),
从而a2=b2+1=4,∴该椭圆的方程为![]()
(2)设A(x1,y1),B(x2,y2),代入椭圆方程可得,
3x12+4y12=12,3x22+4y22=12,
相减可得3(x1﹣x2)(x1+x2)+4(y1﹣y2)(y1+y2)=0,
由x1+x2=2,y1+y2=1,可得直线AB的斜率为![]() ,
,
即直线AB的方程为![]() ,即为3x+2y﹣4=0.
,即为3x+2y﹣4=0.

【题目】某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
[20,30) | 30 | 18 |
[30,40) | 36 | 24 |
[40,50) | 12 | 9 |
[50,60] | 4 | 3 |
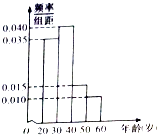
(1)若用分层抽样法从全校教师中抽取一个容量为40的样本,求从年龄段[20,30)抽取的人数;
(2)求全校教师的平均年龄;
(3)随机从年龄段[20,30)和[30,40)内各抽取1人,设这两人中两项培训结业考试成绩都优秀的人数为X,求X的概率分布和数学期望.