Question

【题目】某学校有120名教师，且年龄都在20岁到60岁之间，各年龄段人数按分组，其频率分布直方图如图所示，学校要求每名教师都要参加两项培训，培训结束后进行结业考试．已知各年龄段两项培训结业考试成绩优秀的人数如表示，假设两项培训是相互独立的，结业考试成绩也互不影响．

年龄分组	A项培训成绩优秀人数	B项培训成绩优秀人数
[20，30）	30	18
[30，40）	36	24
[40，50）	12	9
[50，60]	4	3

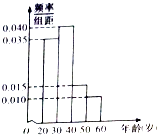
（1）若用分层抽样法从全校教师中抽取一个容量为40的样本，求从年龄段[20，30）抽取的人数；
（2）求全校教师的平均年龄；
（3）随机从年龄段[20，30）和[30，40）内各抽取1人，设这两人中两项培训结业考试成绩都优秀的人数为X，求X的概率分布和数学期望．

Answer 1

【答案】
（1）解：由频率分布直方图知，0.35×40=14
（2）解：由频率分布直方图得：

全校教师的平均年龄为：

25×0.35+35×0.4+45×0.15+55×0.1=35

（3）解：∵在年龄段[20，30）内的教师人数为120×0.35=42（人），从该年龄段任取1人，

由表知，此人A项培训结业考试成绩优秀的概率为 ，

B项培训结业考试成绩优秀的概率为 ，

∴此人A、B两项培训结业考试成绩都优秀的概率为 ，

∵在年龄段[30，40）内的教师人数为120×0.4=48（人），

从该年龄段任取1人，由表知，此人A项培训结业考试成绩优秀的概率为 ，

B项培训结业考试成绩优秀的概率为 ，

∴此人A、B两项培训结业考试成绩都优秀的概率为

由题设知X的可能取值为0，1，2．

∴ ，

，

∴X的概率分布为

X	0	1	2
P

X的数学期望为

【解析】（1）由频率分布直方图能求出从年龄段[20，30）抽取的人数．（2）由频率分布直方图能求出全校教师的平均年龄．（3）由题设知X的可能取值为0，1，2．分别求出相应的概率，由此能求出X的概率分布列和数学期望．
【考点精析】掌握频率分布直方图和离散型随机变量及其分布列是解答本题的根本，需要知道频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息；在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列．