题目内容
【题目】直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D. 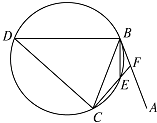
(1)证明:DB=DC;
(2)设圆的半径为1,BC=3,延长CE交AB于点F,求△BCF外接圆的半径.
【答案】
(1)证明:连结DE,交BC于点G.
由弦切角定理得,∠ABE=∠BCE.
而∠ABE=∠CBE,
故∠CBE=∠BCE,BE=CE.
又因为DB⊥BE,
所以DE为直径,∠DCE=90°,
由勾股定理可得DB=DC
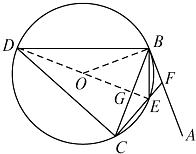
(2)解:由(1)知,∠CDE=∠BDE,DB=DC,
故DG是BC的中垂线,
所以BG= ![]() .
.
设DE的中点为O,连结BO,则∠BOG=60°.
从而∠ABE=∠BCE=∠CBE=30°,
所以CF⊥BF,
故Rt△BCF外接圆的半径等于 ![]() .
.
【解析】(1)构造辅助线DE,交BC于点G.由弦切角定理,圆上的同弧,等弧的性质,通过导角,可以得知∠CBE=∠BCE,BE=CE,又因为DE为直径,即∠DCE=90°,由勾股定理可证得DB=DC;(2)由(1)可得DG是BC的中垂线,即可求得BG的长度.设DE的中点为O,连结BO,求得∠BOG=60°,通过导角,可得CF⊥BF,即可求得Rt△BCF外接圆的半径.

练习册系列答案
相关题目