题目内容
【题目】已知函数![]() ,
,![]()
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)是否存在实数![]() 使得
使得![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)由函数的解析式可得 1﹣![]() >0,即
>0,即 ![]() >0,由此求得定义域,定义域关于原点对称,且f(﹣x)+f(x)=0,可得f(x)是奇函数.
>0,由此求得定义域,定义域关于原点对称,且f(﹣x)+f(x)=0,可得f(x)是奇函数.
(2)a>1时,根据函数f(x)在[m,n]上是增函数,可得函数的值域不可能为[1+logan,1+logam],此时,a不存在.
0<a<1时,f(x)单调递减,则由![]() =1+logax,可得ax2+(2a﹣1)x+2=0.由题意可得,ax2+(2a﹣1)x+2=0有两个大于2的不等实根.根据二次函数的性质求得a的范围.
=1+logax,可得ax2+(2a﹣1)x+2=0.由题意可得,ax2+(2a﹣1)x+2=0有两个大于2的不等实根.根据二次函数的性质求得a的范围.
(1)定义域为{x|x<-2或x>2}, 且![]() ,所以f(x)是奇函数.
,所以f(x)是奇函数.
(2)a>1时,根据函数f(x)在[m,n]上是增函数,1+logan>1+logam,可得函数的值域不可能为[1+logan,1+logam],此时,a不存在.
0<a<1时,f(x)单调递减,则![]() =
=![]()
![]()
![]()
即![]() 有两个大于2的不等实根,
有两个大于2的不等实根,
设g(x)= ![]() ,则
,则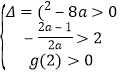 , 解得
, 解得![]() .
.

练习册系列答案
相关题目