题目内容
已知抛物线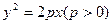 的焦点为F,A是抛物线上横坐标为4、且位于
的焦点为F,A是抛物线上横坐标为4、且位于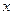 轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于
轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于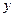 轴,垂足为B,OB的中点为M.
轴,垂足为B,OB的中点为M.
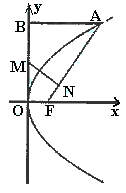
(1)求抛物线方程;
(2)过M作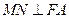 ,垂足为N,求点N的坐标;
,垂足为N,求点N的坐标;
(3)以M为圆心,MB为半径作圆M,当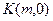 是
是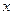 轴上一动点时,讨论直线AK与圆M的位置关系.
轴上一动点时,讨论直线AK与圆M的位置关系.
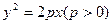 的焦点为F,A是抛物线上横坐标为4、且位于
的焦点为F,A是抛物线上横坐标为4、且位于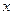 轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于
轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于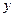 轴,垂足为B,OB的中点为M.
轴,垂足为B,OB的中点为M.
(1)求抛物线方程;
(2)过M作
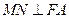 ,垂足为N,求点N的坐标;
,垂足为N,求点N的坐标;(3)以M为圆心,MB为半径作圆M,当
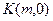 是
是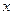 轴上一动点时,讨论直线AK与圆M的位置关系.
轴上一动点时,讨论直线AK与圆M的位置关系.抛物线方程为y2= 4x. 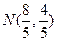
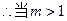 时,直线AK与圆M相离;当m=1时,直线AK与圆M相切;
时,直线AK与圆M相离;当m=1时,直线AK与圆M相切;
当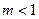 时,直线AK与圆M相交.
时,直线AK与圆M相交.
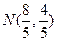
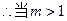 时,直线AK与圆M相离;当m=1时,直线AK与圆M相切;
时,直线AK与圆M相离;当m=1时,直线AK与圆M相切;当
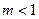 时,直线AK与圆M相交.
时,直线AK与圆M相交.(1)抛物线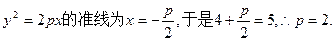
∴抛物线方程为y2= 4x.
(2)∵点A的坐标是(4,4),由题意得B(0,4),M(0,2),
又∵F(1,0),∴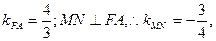
则FA的方程为y=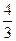 (x-1),MN的方程为
(x-1),MN的方程为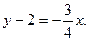
解方程组
(3)由题意得,圆M的圆心是点(0,2),半径为2.
当m=4时,直线AK的方程为x=4,此时,直线AK与圆M相离,
当m≠4时,直线AK的方程为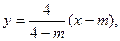 即为
即为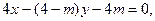
圆心M(0,2)到直线AK的距离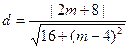 ,令
,令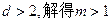
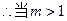 时,直线AK与圆M相离;
时,直线AK与圆M相离;
当m=1时,直线AK与圆M相切;
当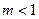 时,直线AK与圆M相交.
时,直线AK与圆M相交.
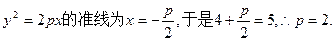
∴抛物线方程为y2= 4x.
(2)∵点A的坐标是(4,4),由题意得B(0,4),M(0,2),
又∵F(1,0),∴
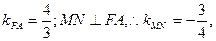
则FA的方程为y=
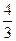 (x-1),MN的方程为
(x-1),MN的方程为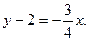
解方程组

(3)由题意得,圆M的圆心是点(0,2),半径为2.
当m=4时,直线AK的方程为x=4,此时,直线AK与圆M相离,
当m≠4时,直线AK的方程为
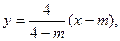 即为
即为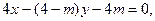
圆心M(0,2)到直线AK的距离
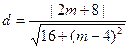 ,令
,令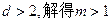
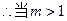 时,直线AK与圆M相离;
时,直线AK与圆M相离;当m=1时,直线AK与圆M相切;
当
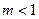 时,直线AK与圆M相交.
时,直线AK与圆M相交.
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
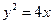 上一点P(
上一点P(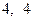 ),作两条直线分别交抛物线于A(
),作两条直线分别交抛物线于A(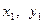 ),B(
),B(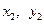 ).直线PA与PB的斜率存在且互为相反数,(1)求
).直线PA与PB的斜率存在且互为相反数,(1)求 的值,(2)证明直线AB的斜率是非零常数.
的值,(2)证明直线AB的斜率是非零常数.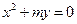 上的点到定点
上的点到定点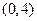 和到定直线
和到定直线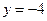 的距离相等,则
的距离相等,则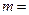
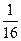 ;
;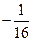 ;
;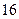 ;
;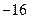 .
.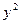 =2px(p>0)的焦点F的
=2px(p>0)的焦点F的 直线
直线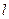 与抛物线在第一象限的交点为A,与抛物线准线的交点为B,点A在抛物线准线上的射影为C,若
与抛物线在第一象限的交点为A,与抛物线准线的交点为B,点A在抛物线准线上的射影为C,若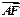 =
=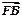 ,
,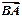 ·
·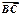 =48,则抛物线的方程为______________。
=48,则抛物线的方程为______________。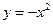 上的点到直线
上的点到直线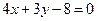 距离的最小值是( )
距离的最小值是( )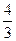
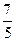
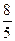
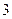
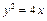 的准线与双曲线
的准线与双曲线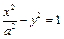 交于A、B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线的离心率为 .
交于A、B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线的离心率为 .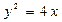 上一点P引抛物线准线的垂线,垂足为
上一点P引抛物线准线的垂线,垂足为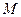 且
且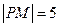 ,设抛物线的焦点为F,则
,设抛物线的焦点为F,则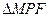 的面积为( )
的面积为( )
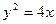 的焦点F交抛物线于A
的焦点F交抛物线于A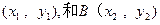 ,
,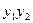 =
=