题目内容
【题目】如图,四棱锥![]() 的底面
的底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]() ,
,![]() .
.
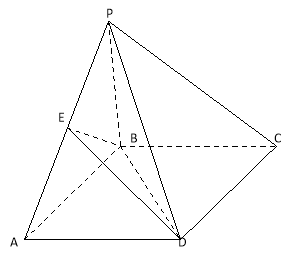
(I)求证:![]() 平面
平面![]() ;
;
(II)求三棱锥![]() 的体积.
的体积.
【答案】(I)详见解析(II)![]()
【解析】
![]() 试题分析:(I)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证,往往需要利用平几知识,如本题利用三角形中位线得:连接
试题分析:(I)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证,往往需要利用平几知识,如本题利用三角形中位线得:连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() (II)求三棱锥的体积,关键在求高,而高一般通过线面垂直得到,本题可以面面垂直性质定理可得线面垂直:利用等腰三角形性质可得
(II)求三棱锥的体积,关键在求高,而高一般通过线面垂直得到,本题可以面面垂直性质定理可得线面垂直:利用等腰三角形性质可得![]() (
(![]() 为
为![]() 中点),再利用面面垂直性质定理可得
中点),再利用面面垂直性质定理可得![]() 平面
平面![]() .在三角形中求出PH值,及三角形PBD面积,代入体积公式得结果
.在三角形中求出PH值,及三角形PBD面积,代入体积公式得结果
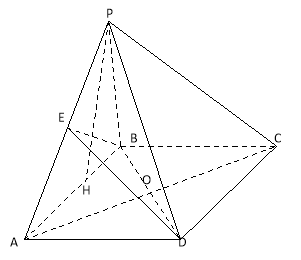
试题解析:解:(I)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() 是
是![]() 的中点.
的中点.
又∵![]() 是
是![]() 的中点,∴
的中点,∴![]() 是
是![]() 的中位线,∴
的中位线,∴![]() ,
,
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(II)取![]() 中点
中点![]() ,连接
,连接![]() ,
,
由![]() 得
得![]() ,
,
又∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 是边长为2的等边三角形,∴
是边长为2的等边三角形,∴![]() ,
,
又∵![]() ,
,
∴![]()

练习册系列答案
相关题目
【题目】已知![]() 三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
(1)试估计![]() 班学生人数;
班学生人数;
(2)从![]() 班和
班和![]() 班抽出来的学生中各选一名,记
班抽出来的学生中各选一名,记![]() 班选出的学生为甲,
班选出的学生为甲,![]() 班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.