题目内容
气象部门提供了某地今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t (单位:℃) | t 22℃ 22℃ | 22℃<t 28℃ 28℃ | 28℃<t 32℃ 32℃ | 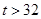 ℃ ℃ |
| 天数 | 6 | 12 | 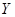 | 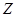 |
某水果商根据多年的销售经验,六月份的日最高气温t (单位:℃)对西瓜的销售影响如下表:
| 日最高气温t (单位:℃) | t 22℃ 22℃ | 22℃<t 28℃ 28℃ | 28℃<t 32℃ 32℃ | 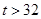 ℃ ℃ |
日销售额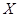 (千元) (千元) | 2 | 5 | 6 | 8 |
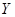 ,
, 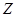 的值;
的值;(Ⅱ) 若视频率为概率,求六月份西瓜日销售额的期望和方差;
(Ⅲ) 在日最高气温不高于32℃时,求日销售额不低于5千元的概率.
(Ⅰ)9, 3;(Ⅱ) 5, 3;(Ⅲ)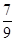 .
.
解析试题分析:(Ⅰ)把频率看作概率,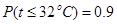 ,根据频率和为1,可求得
,根据频率和为1,可求得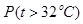 ,在由皮书等于频率
,在由皮书等于频率 样本总数,便求得
样本总数,便求得 ,
, 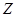 的值;(Ⅱ) 随机变量
的值;(Ⅱ) 随机变量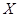 取2,5,6,8,列出六月份西瓜销售额
取2,5,6,8,列出六月份西瓜销售额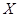 的分布列为,再用公式求六月份西瓜日销售额的期望和方差;(Ⅲ) 利用条件概率的计算公式求解.
的分布列为,再用公式求六月份西瓜日销售额的期望和方差;(Ⅲ) 利用条件概率的计算公式求解.
试题解析:(Ⅰ) 由已知得: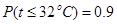 ,
,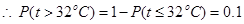
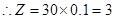 ,
, . 4分
. 4分
(Ⅱ) 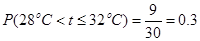
六月份西瓜销售额X的分布列为: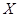
2 5 6 8 P 0.2 0.4 0.3 0.1 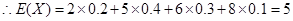 ,
, . 9分
. 9分
(Ⅲ) 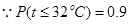 ,
,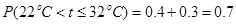
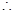 由条件概率得:
由条件概率得: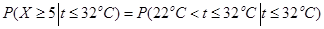
=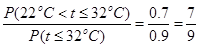 . 12分
. 12分
考点:频率、概率,条件概率,随机变量的分布列、期望与方差.

练习册系列答案
相关题目
已知某校在一次考试中,5名学生的数学和物理成绩如下表:
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学成绩x | 80 | 75 | 70 | 65 | 60 |
| 物理成绩y | 70 | 66 | 68 | 64 | 62 |
(Ⅱ)根据上表,利用最小二乘法,求出
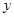 关于
关于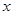 的线性回归方程
的线性回归方程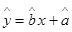 ,
,其中
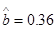
(III)利用(Ⅱ)中的线性回归方程,试估计数学90分的同学的物理成绩.(四舍五入到整数)
 其中
其中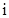 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响). 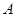 “在一次试验中,得到的数为虚数”的概率
“在一次试验中,得到的数为虚数”的概率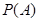 与事件
与事件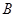 “在四次试验中,
“在四次试验中,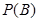 ;
;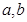 ,求随机变量
,求随机变量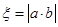 的分布列与数学期望
的分布列与数学期望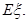
 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求
 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求
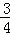 、
、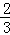 、
、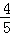 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场. (如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为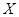 .若
.若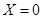 就参加学校合唱团,否则就参加学校排球队.
就参加学校合唱团,否则就参加学校排球队.
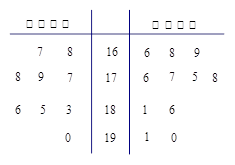
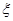 表示乙校中选出的“高个子”人数,试求出
表示乙校中选出的“高个子”人数,试求出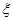 ,求随机变量
,求随机变量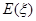 .
.