题目内容
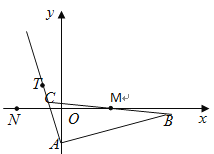
【题目】已知抛物线C：y2=2px（p＞0）和动直线l：y=kx+b（k，b是参变量，且k≠0．b≠0）相交于A（x1 ， y2），N）x2 ， y2）两点，直角坐标系原点为O，记直线OA，OB的斜率分别为kOAkOB= 
恒成立，则当k变化时直线l恒经过的定点为（ ）
A.（﹣ p，0）
B.（﹣2 p，0）
C.（﹣ 
，0）
D.（﹣ 
，0）
【答案】D
【解析】解：将直线与抛物线联立，消去y，得k2x2+（2kb﹣2p）x+b2=0， ∴x1+x2= 
，x1x2= 
；
∵kOAkOB= 
，∴y1y2= x1x2 ，
∴y1y2=（kx1+b）（kx2+b）
=k2x1x2+kb（x1+x2）+b2
= 
；
∴ = ，
解得b= 
，
∴y=kx+ =k（x+ 
）
令x=﹣ ，得y=0，
∴直线过定点（﹣ ，0）．
故选D．
练习册系列答案
应用题作业本系列答案
相关题目
【题目】现有1000根某品种的棉花纤维，从中随机抽取50根，纤维长度（单位：mm）的数据分组及各组的频数如表，据此估计这1000根中纤维长度不小于37.5mm的根数是 ．
纤维长度 | 频数 |
[22.5，25.5） | 3 |
[25.5，28.5） | 8 |
[28.5，31.5） | 9 |
[31.5，34.5） | 11 |
[34.5，37.5） | 10 |
[37.5，40.5） | 5 |
[40.5，43.5] | 4 |
