题目内容
【题目】如图，在△ABC中，∠B=30°，AC= 
，D是边AB上一点．
（1）求△ABC面积的最大值；
（2）若CD=2，△ACD的面积为2，∠ACD为锐角，求BC的长．
【答案】
（1）解：∵ 
，
∴由余弦定理可得：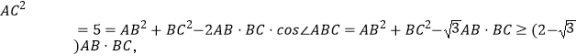 
∴ 
∴ 
，
所以△ABC的面积的最大值为 
（2）解：设∠ACD=θ，在△ACD中， 
，
∴ 
，解得： 
，∴ 
由余弦定理得： 
，
∴ 
，
∵ 
，∴ 
，
∴ 
，此时 
，
∴ 
【解析】（1）由已知及余弦定理，基本不等式可得 ，利用三角形面积公式即可得解△ABC的面积的最大值．（2）设∠ACD=θ，利用三角形面积公式可解得 ，可求 ，由余弦定理得即可解得AD的值，利用正弦定理可求sinA，进而利用正弦定理可求BC的值．
【考点精析】根据题目的已知条件，利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案，需要掌握正弦定理:
；余弦定理:
;
;
．
练习册系列答案
相关题目
【题目】某商店为了更好地规划某种商品进货的量，该商店从某一年的销售数据中，随机抽取了
组数据作为研究对象，如下图所示（
（吨）为该商品进货量， 
（天）为销售天数）：
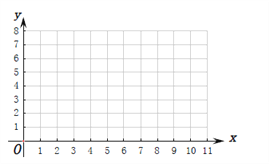
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
（Ⅰ）根据上表数据在下列网格中绘制散点图；
（Ⅱ）根据上表提供的数据，求出关于的线性回归方程
；
（Ⅲ)在该商品进货量
（吨）不超过6（吨）的前提下任取两个值，求该商品进货量x（吨）恰有一个值不超过3（吨）的概率.
参考公式和数据：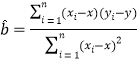
，
．
