题目内容
【题目】已知x1 ， x2是函数f（x）=2sin2x+cos2x﹣m在[0， 
]内的两个零点，则sin（x1+x2）= ．
【答案】
【解析】解：x1 ， x2是函数f（x）=2sin2x+cos2x﹣m在[0， 
]内的两个零点， 可得m=2sin2x1+cos2x1=2sin2x2+cos2x2 ，
即为2（sin2x1﹣sin2x2）=﹣cos2x1+cos2x2 ，
即有4cos（x1+x2）sin（x1﹣x2）=﹣2sin（x2+x1）sin（x2﹣x1），
由x1≠x2 ， 可得sin（x1﹣x2）≠0，
可得sin（x2+x1）=2cos（x1+x2），
由sin2（x2+x1）+cos2（x1+x2）=1，
可得sin（x2+x1）=± ，
由x1+x2∈[0，π]，
即有sin（x2+x1）= ．
所以答案是： ．
名题金卷系列答案
优加精卷系列答案【题目】某商场为一种跃进商品进行合理定价，将该商品按事先拟定的价格进行试销，得到如下数据：
单位 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
（1）按照上述数据，求四归直线方程
，其中
，
；
（2）预计在今后的销售中，销量与单位仍然服从（Ⅰ）中的关系，若该商品的成本是每件7.5元，为使商场获得最大利润，该商品的单价应定为多少元？（利润=销售收入﹣成本）
【题目】某商店为了更好地规划某种商品进货的量，该商店从某一年的销售数据中，随机抽取了
组数据作为研究对象，如下图所示（
（吨）为该商品进货量， 
（天）为销售天数）：
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
（Ⅰ）根据上表数据在下列网格中绘制散点图；
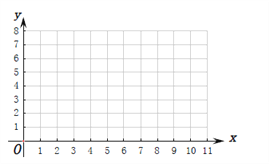
（Ⅱ）根据上表提供的数据，求出关于的线性回归方程
；
（Ⅲ)在该商品进货量
（吨）不超过6（吨）的前提下任取两个值，求该商品进货量x（吨）恰有一个值不超过3（吨）的概率.
参考公式和数据：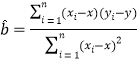
，
．