题目内容
3.圆锥的体积为$\frac{2\sqrt{2}}{3}$π,底面积为π,则该圆锥侧面展开图的圆心角大小为$\frac{2π}{3}$.分析 根据已知,求出圆锥的底面半径和母线长,进而可得该圆锥侧面展开图的圆心角大小.
解答 解:∵圆锥的底面积为π,
故圆锥的底面半径r=1,
又∵圆锥的体积为$\frac{2\sqrt{2}}{3}$π,
故圆锥的高h=2$\sqrt{2}$,
故圆锥的母线长l=$\sqrt{{r}^{2}+{h}^{2}}$=3,
设该圆锥侧面展开图的圆心角大小为θ,
则$\frac{θ}{2π}=\frac{r}{l}$=$\frac{1}{3}$,
故θ=$\frac{2π}{3}$,
故答案为:$\frac{2π}{3}$
点评 本题考查的知识点是旋转体,圆锥的体积公式,圆锥的展开图,难度不大,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
11.已知函数f(x)=cos2x-sin2x,下列结论中错误的是( )
| A. | f(x)=cos2x | B. | f(x)的最小正周期为π | ||
| C. | f(x)的图象关于直线x=0对称 | D. | f(x)的值域为[-$\sqrt{2}$,$\sqrt{2}$] |
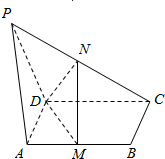 如图,PA⊥平面ABCD,ABCD是矩形,M、N分别是AB,PC的中点.
如图,PA⊥平面ABCD,ABCD是矩形,M、N分别是AB,PC的中点. 如图,在△ABC中,若AB,BC在平面α内,试判断AC是否在平面α内.
如图,在△ABC中,若AB,BC在平面α内,试判断AC是否在平面α内.