题目内容
11.已知函数f(x)=cos2x-sin2x,下列结论中错误的是( )| A. | f(x)=cos2x | B. | f(x)的最小正周期为π | ||
| C. | f(x)的图象关于直线x=0对称 | D. | f(x)的值域为[-$\sqrt{2}$,$\sqrt{2}$] |
分析 由平方差公式及二倍角的余弦函数公式化简函数解析式可得f(x)=cos2x,利用余弦函数的图象和性质及余弦函数的周期公式即可得解.
解答 解:由f(x)=cos4x-sin4x=(cos2x+sin2x)(cos2x-sin2x)=cos2x,故A正确;
由周期公式可得f(x)的最小正周期为:T=$\frac{2π}{2}=π$,故B正确;
由利用余弦函数的图象可知f(x)=cos2x为偶函数,故C正确;
由余弦函数的性质可得f(x)=cos2x的值域为[-1,1],故D错误;
故选:D.
点评 本题主要考查了平方差公式及二倍角的余弦函数公式,考查了余弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
6.若不等式mx2-mx+2>0对一切实数x恒成立,则实数m的取值范围是( )
| A. | (0,8) | B. | [0,8] | C. | [0,8) | D. | (0,8] |
1.设α为锐角,则“tanα>2”是“-$\frac{4}{3}$<tan2α<0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
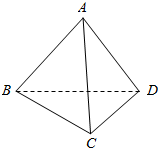 在空间四边形ABCD中,设AB⊥CD,AC⊥BD.
在空间四边形ABCD中,设AB⊥CD,AC⊥BD.