Question

13．已知函数f_t（x）=（x-t）²-t（t∈R），设a＜b，f（x）=$\left\{\begin{array}{l}{f_a}（x），{f_a}（x）＜{f_b}（x）\\{f_b}（x），{f_a}（x）≥{f_b}（x）\end{array}$，若函数y=f（x）+x+a-b有三个零点，则b-a的值为2+$\sqrt{5}$．

Answer 1

分析 解方程f_a（x）=f_b（x）得交点坐标，函数f（x）的图象与直线l：y=-x+b-a有三个不同的交点，由图象知，点P在l上，故，由此解得b-a的取值．

解答 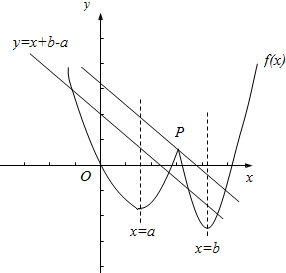解：作函数f（x）的图象，且解方程f_a（x）=f_b（x）得，
（x-a）²-a=（x-b）²-b，解得x=$\frac{a+b-1}{2}$，此时y=（$\frac{a+b-1}{2}$-a）²-a=（$\frac{b-a-1}{2}$）²-a，
即交点坐标为（$\frac{a+b-1}{2}$，（$\frac{b-a-1}{2}$）²-a），
若y=f（x）+x+a-b有三个零点，
即f（x）+x+a-b=0有三个根，
即f（x）=-x+b-a，
分别作出f（x）与y=-x+b-a的图象如图：
要使函数y=f（x）+x+a-b有三个零点，
即函数f（x）的图象与直线l：y=-x+b-a有三个不同的交点．
由图象知，点P在l上，
所以（$\frac{b-a-1}{2}$）²-a=-$\frac{a+b-1}{2}$+b-a，
即（$\frac{b-a-1}{2}$）²=$\frac{b-a+1}{2}$，
设t=b-a，则t＞0，
则方程等价为$\frac{（t-1）^{2}}{4}=\frac{t+1}{2}$，即t²-4t-1=0，
即t=2±$\sqrt{5}$，
∵t＞0，∴t=2+$\sqrt{5}$，即b-a=2+$\sqrt{5}$，
故答案为：2+$\sqrt{5}$．

点评 本题主要考查根的存在性以及根的个数判断，函数的零点与方程的根的关系，体现了转化的数学思想，利用数形结合是解决本题的关键．