题目内容
15.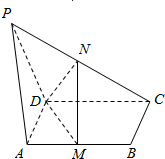 如图,PA⊥平面ABCD,ABCD是矩形,M、N分别是AB,PC的中点.
如图,PA⊥平面ABCD,ABCD是矩形,M、N分别是AB,PC的中点.(1)求证:MN⊥AB;
(2)若PA=AD,求证:平面MND⊥平面PDC.
分析 (1)可由条件得到AB,AD,AP三直线两两垂直,从而可分别以这三直线为x,y,z轴,建立空间直角坐标系,然后设AB=2a,AD=2b,AP=2c,这样便可求出图形上各点的坐标,从而可以得出向量$\overrightarrow{MN},\overrightarrow{AB}$的坐标,求出$\overrightarrow{MN}•\overrightarrow{AB}=0$便得到MN⊥AB;
(2)PA=AD时,由(1)便知b=c,将(1)中各点坐标中的c都换上b,从而可以求出向量$\overrightarrow{MN},\overrightarrow{MD},\overrightarrow{DC},\overrightarrow{DP}$的坐标,可设平面MND的法向量为$\overrightarrow{m}=({x}_{1},{y}_{1},{z}_{1})$,从而由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{DM}=0}\\{\overrightarrow{m}•\overrightarrow{DN}=0}\end{array}\right.$便可求出向量$\overrightarrow{m}$的坐标,同理求出向量$\overrightarrow{n}$的坐标,然后证明$\overrightarrow{m}•\overrightarrow{n}=0$,便得出$\overrightarrow{m}⊥\overrightarrow{n}$,从而证出平面MND⊥平面PDC.
解答 证明:(1)根据条件知AB,AD,AP三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,设AB=2a,AD=2b,AP=2c,则: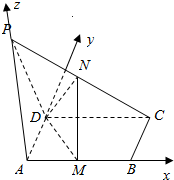
A(0,0,0),B(2a,0,0),C(2a,2b,0),D(0,2b,0),P(0,0,2c),M(a,0,0),N(a,b,c);
∴$\overrightarrow{AB}=(2a,0,0),\overrightarrow{MN}=(0,b,c)$;
∴$\overrightarrow{AB}•\overrightarrow{MN}=0$;
∴$\overrightarrow{AB}⊥\overrightarrow{MN}$;
即MN⊥AB;
(2)若PA=AD,则b=c,则D(0,2b,0),M(a,0,0),N(a,b,b),C(2a,2b,0),P(0,0,2b);
∴$\overrightarrow{MN}=(0,b,b),\overrightarrow{MD}=(-a,2b,0)$,$\overrightarrow{DC}=(2a,0,0),\overrightarrow{DP}=(0,-2b,2b)$;
设平面MND的法向量为$\overrightarrow{m}=({x}_{1},{y}_{1},{z}_{1})$,则:
$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{MN}=b({y}_{1}+{z}_{1})=0}\\{\overrightarrow{m}•\overrightarrow{MD}=-a{x}_{1}+2b{y}_{1}=0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{{y}_{1}=-{z}_{1}}\\{{x}_{1}=-\frac{2b}{a}{z}_{1}}\end{array}\right.$;
取z1=1,则$\overrightarrow{m}=(-\frac{2b}{a},-1,1)$;
同理设平面PDC的法向量为$\overrightarrow{n}=({x}_{2},{y}_{2},{z}_{2})$,由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DC}=2a{x}_{2}=0}\\{\overrightarrow{n}•\overrightarrow{DP}=-2b({y}_{2}-{z}_{2})=0}\end{array}\right.$,取z2=1得:$\overrightarrow{n}=(0,1,1)$;
∴$\overrightarrow{m}•\overrightarrow{n}=-1+1=0$;
∴$\overrightarrow{m}⊥\overrightarrow{n}$;
∴平面MND⊥平面PDC.
点评 考查通过建立空间坐标系,利用空间向量解决立体几何问题的方法,能求空间点的坐标,由点的坐标可求空间向量的坐标,向量垂直的充要条件,以及平面法向量的概念及求法,清楚两平面垂直时法向量的关系.

| A. | (0,8) | B. | [0,8] | C. | [0,8) | D. | (0,8] |
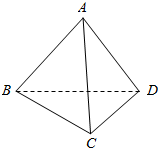 在空间四边形ABCD中,设AB⊥CD,AC⊥BD.
在空间四边形ABCD中,设AB⊥CD,AC⊥BD.