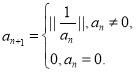题目内容
【题目】定义在R上的奇函数![]() ,当
,当![]() 时,
时, 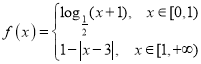
则函数![]() 的所有零点之和为_____.
的所有零点之和为_____.
【答案】![]()
【解析】
函数F(x)=f(x)﹣a(0<a<1)的零点转化为:在同一坐标系内y=f(x),y=a的图象交点的横坐标;作出两函数图象,考查交点个数,结合方程思想,及零点的对称性,根据奇函数f(x)在x≥0时的解析式,作出函数的图象,结合图象及其对称性,求出答案.
∵当x≥0时,
f(x)=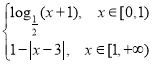
即x∈[0,1)时,f(x)=![]() (x+1)∈(﹣1,0];
(x+1)∈(﹣1,0];
x∈[1,3]时,f(x)=x﹣2∈[﹣1,1];
x∈(3,+∞)时,f(x)=4﹣x∈(﹣∞,﹣1);
画出x≥0时f(x)的图象,
再利用奇函数的对称性,画出x<0时f(x)的图象,如图所示;
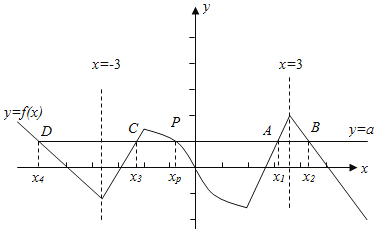
则直线y=a,与y=f(x)的图象有5个交点,则方程f(x)﹣a=0共有五个实根,
最左边两根之和为﹣6,最右边两根之和为6,
∵x∈(﹣1,0)时,﹣x∈(0,1),
∴f(﹣x)=![]() (﹣x+1),
(﹣x+1),
又f(﹣x)=﹣f(x),
∴f(x)=﹣![]() (﹣x+1)=
(﹣x+1)=![]() (1﹣x)﹣1=log2(1﹣x),
(1﹣x)﹣1=log2(1﹣x),
∴中间的一个根满足log2(1﹣x)=a,即1﹣x=2a,
解得x=1﹣2a,
∴所有根的和为1﹣2a.
故答案为:1﹣2a.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目