��Ŀ����
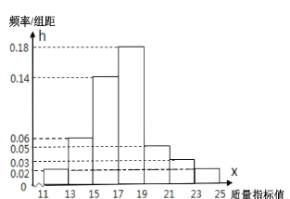
����Ŀ����ij��ҵ��ij�ֲ�Ʒ�г�ȡ![]() ����������Щ��Ʒ��һ������ָ��ֵ���ɲ������������Ƶ�ʷֲ�ֱ��ͼ��
����������Щ��Ʒ��һ������ָ��ֵ���ɲ������������Ƶ�ʷֲ�ֱ��ͼ��
��������![]() ����Ʒ����ָ��ֵ������ƽ����
����Ʒ����ָ��ֵ������ƽ����![]() ����������
����������![]() ��ͬһ�������ø�������е�ֵ������������
��ͬһ�������ø�������е�ֵ������������![]() ��
��![]() ����
����
������Ƶ�ʷֲ�ֱ��ͼ������Ϊ�����ֲ�Ʒ������ָ��ֵ![]() ������̬�ֲ�
������̬�ֲ�![]() ������
������![]() ����Ϊ����ƽ����
����Ϊ����ƽ����![]() ��
��![]() ������������
������������![]() ��
��
��i����ʹ![]() �IJ�Ʒ������ָ��ֵ������ҵ�ƶ��ĺϸ������ϸ��������ָ��ֵ��ԼΪ���٣�
�IJ�Ʒ������ָ��ֵ������ҵ�ƶ��ĺϸ������ϸ��������ָ��ֵ��ԼΪ���٣�
��ii��������ҵ�����������ֲ�Ʒ![]() ������ÿ����Ʒ�����������
������ÿ����Ʒ�����������![]() ����Ʒ����ָ��ֵ������
����Ʒ����ָ��ֵ������![]() �ļ������п����Ƕ��٣�
�ļ������п����Ƕ��٣�
�����ο������빫ʽ��![]() ��
��![]() ����
����![]() �����
�����![]() ����
����![]() ����
����![]() ��
��
���𰸡�����![]() ��
��![]() ������i��
������i��![]() ����ii��
����ii��![]() ��
��
��������
������Ƶ�ʷֲ�ֱ��ͼ����ƽ�����ķ�����ֱ�����![]() �����÷�����㹫ʽ
�����÷�����㹫ʽ![]() ����������������i������
����������������i������![]() ԭ�����֤��
ԭ�����֤��![]() �����
�����![]() ���������ii������
��Ϊ�������ii������![]() ԭ��ɵõ�
ԭ��ɵõ�![]() ���Ӷ��õ���
���Ӷ��õ���![]() ��Ʒ������ָ��ֵ������
��Ʒ������ָ��ֵ������![]() �ļ���
�ļ���![]() ������
������![]() ��
��![]() �����ݶ���ֲ����ʹ�ʽ���첻��ʽ
�����ݶ���ֲ����ʹ�ʽ���첻��ʽ ���ⲻ��ʽ�����
���ⲻ��ʽ�����![]() ���Ӷ��ɵý��.
���Ӷ��ɵý��.
����
![]()
![]()
����������֪��![]()
��i��![]()
��![]() ʱ����������
ʱ����������
���ϸ��������ָ��ֵԼΪ��![]()
��ii����![]()
��֪ÿ����Ʒ������ָ��ֵ������![]() ���¼�����Ϊ
���¼�����Ϊ![]()
����![]() ��Ʒ������ָ��ֵ������
��Ʒ������ָ��ֵ������![]() �ļ���Ϊ
�ļ���Ϊ![]()
��![]() ������
������![]()
![]() ǡ��
ǡ��![]() ����Ʒ������ָ��ֵ������
����Ʒ������ָ��ֵ������![]() ���¼����ʣ�
���¼����ʣ�![]()
��![]() ����ã�
����ã�![]()
![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]()
�ɴ˿�֪������![]() ����Ʒ�У�����ָ��ֵ������
����Ʒ�У�����ָ��ֵ������![]() �ļ������п�����
�ļ������п�����![]()

����Ŀ��2018 ��1��16�գ����»������й��ƾ������������������2017�й��ƾ����������ѡ���������ij֪����վ�ƾ�Ƶ��Ϊ�˽�ڶ���Щ��������Ƿ��˽⣬��������ƽ̨�����˵��飬���Ӳ�������������ѡ��![]() �ˣ�����
�ˣ�����![]() �˷�Ϊ
�˷�Ϊ![]() ���ࣨ
���ࣨ![]() ���ʾ����Щ�������Ƚ��˽⣬
���ʾ����Щ�������Ƚ��˽⣬![]() ���ʾ����Щ������ﲻ̫�˽⣩�����Ƴ����±���
���ʾ����Щ������ﲻ̫�˽⣩�����Ƴ����±���
����� |
|
|
|
|
���� |
|
|
|
|
|
|
|
|
|
��1������������ν��зֲ����������![]() ����ѡ��
����ѡ��![]() �˽��з�̸��������
�˽��з�̸��������![]() �������ѡ�����������߸��轱��.������һ�������ߵ�������
�������ѡ�����������߸��轱��.������һ�������ߵ�������![]() �ꡫ
�ꡫ![]() ��֮�䣬��һ�������ߵ�������
��֮�䣬��һ�������ߵ�������![]() �ꡫ
�ꡫ![]() ��֮��ĸ��ʣ�(ע����
��֮��ĸ��ʣ�(ע����![]() �������ѡ��
�������ѡ��![]() ��,����
��,����![]() �ֲ�ͬѡ��)
�ֲ�ͬѡ��)
��2�������������![]() �ꡫ
�ꡫ![]() ��֮����˳�Ϊ�����꣬������
��֮����˳�Ϊ�����꣬������![]() �ꡫ
�ꡫ![]() ��֮����˳�Ϊ�����꣬���ܷ��ڷ�����ĸ��ʲ�����
��֮����˳�Ϊ�����꣬���ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ�����������������ڶԲƾ����������˽�̶����в��죿
��ǰ������Ϊ�����������������ڶԲƾ����������˽�̶����в��죿
�ο����ݣ�
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ������
������![]()