题目内容
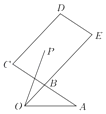
【题目】某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:![]() ):男生成绩在175
):男生成绩在175![]() 以上(包括175
以上(包括175![]() )定义为“合格”,成绩在175
)定义为“合格”,成绩在175![]() 以下(不包括175
以下(不包括175![]() )定义为“不合格”.女生成绩在165
)定义为“不合格”.女生成绩在165![]() 以上(包括165
以上(包括165![]() )定义为“合格”,成绩在165
)定义为“合格”,成绩在165![]() 以下(不包括165
以下(不包括165![]() )定义为“不合格”.
)定义为“不合格”.
(1)求五年一班的女生立定跳远成绩的中位数;
(2)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(3)若从五年一班成绩“合格”的学生中选取2人参加复试,用![]() 表示其中男生的人数,写出
表示其中男生的人数,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
【答案】(1)166.5cm (2) ![]() (3)见解析
(3)见解析
【解析】
(1)按照中位数的定义,可以根据茎叶图得到五年一班的女生立定跳远成绩的中位数;
(2) 男生中任意选取3人,至少有2人的成绩是合格,包括两个事件:一个为事件![]() :“仅有两人的成绩合格”,另一个为事件
:“仅有两人的成绩合格”,另一个为事件![]() :“有三人的成绩合格”,所以至少有两人的成绩是合格的概率:
:“有三人的成绩合格”,所以至少有两人的成绩是合格的概率:![]() ,分别求出
,分别求出![]() ,最后求出
,最后求出![]() ;
;
(3) 因为合格的人共有18人,其中有女生有10人合格,男生有8人合格,依题意,![]() 的取值为0,1,2,分别求出
的取值为0,1,2,分别求出![]() 的值,最后列出
的值,最后列出![]() 的分布列和计算出
的分布列和计算出![]() 的数学期望.
的数学期望.
解:(1)由茎叶图得五年一班的女生立定跳远成绩的中位数为![]()
(2)设“仅有两人的成绩合格”为事件![]() ,“有三人的成绩合格”为事件
,“有三人的成绩合格”为事件![]() ,
,
至少有两人的成绩是合格的概率:![]() ,
,
又男生共12人,其中有8人合格,从而![]() ,
,
![]() ,所以
,所以![]() .
.
(3)因为合格的人共有18人,其中有女生有10人合格,男生有8人合格,
依题意,![]() 的取值为0,1,2,
的取值为0,1,2,
则![]() ,
,
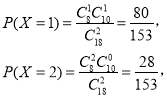
因此,X的分布列如下:
| 0 | 1 | 2 |
|
|
|
|
![]() (人).
(人).
或是,因为![]() 服从超几何分布,所以
服从超几何分布,所以![]() (人).
(人).

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目