题目内容

18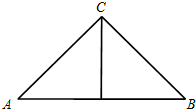．如图，正三棱锥的主视图由等腰直角三角形ABC及斜边AB上的高组成，如果AB=2$\sqrt{3}$，那么这个正三棱锥的体积是（　　）
A．$3\sqrt{3}$B．$\sqrt{3}$C．9D．3

分析 利用三视图求出正四棱锥的底面边长，求出棱锥的高，然后求解体积．

解答 解：由题意可知正四棱锥的底面边长为：$2\sqrt{3}$，
主视图的三角形的高，就是正四棱锥的高，高为：$\sqrt{3}$．
所以这个正三棱锥的体积是：$\frac{1}{3}×\frac{\sqrt{3}}{4}×{（2\sqrt{3}）}^{2}×\sqrt{3}$=3．
故选：D．

点评 本题考查三角锥的体积的求法，直观图与三视图的关系，考查空间想象能力以及计算能力．

练习册系列答案
相关题目
8．△ABC的三边长是三个连续的正整数，M为BC边中点，tanC=$\frac{1}{tan∠BAM}$，求△ABC的形状．
9．方程log2x+x=2的解所在的区间为（　　）
A．（0.5，1）B．（1，1.5）C．（1.5，2）D．（2，2.5）
6．已知集合A={x∈R|x4+mx-2=0}，满足a∈A的所有点M（a，$\frac{2}{a}$）均在直线y=x的同侧，则实数m的取值范围是（　　）
A．（-∞，-$\sqrt{2}$）∪（$\sqrt{2}$，+∞）B．（-$\sqrt{2}$，-1）∪（1，$\sqrt{2}$）C．（-5，-$\sqrt{2}$）∪（$\sqrt{2}$，6）D．（-∞，-6）∪（6，+∞）
13．执行如图所示的程序框图，若输出的k值为5，则输入的整数p的最大值为（　　）
A．7B．31C．15D．63
3．球内接正六棱锥的侧棱长与底面边长分别为$2\sqrt{2}$和2，则该球的体积为$\frac{32}{3}π$．
10．设0＜|α|＜$\frac{π}{4}$，则下列不等式中一定成立的是 （　　）
A．sin2α＞sinαB．cos2α＜cosαC．tan2α＞tanαD．tan2α＜tanα
7．集合A={x|0≤x≤2}，B={x|x2-x＞0}，则A∩B=（　　）
A．RB．（-∞，0）∪（1，2）C．∅D．（1，2]
8．函数y=sinx，x∈[π，2π]的值域是（　　）
A．[-1，1]B．[0，1]C．[-1，0]D．[0，$\frac{1}{2}$]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网