题目内容
3.球内接正六棱锥的侧棱长与底面边长分别为$2\sqrt{2}$和2,则该球的体积为$\frac{32}{3}π$.分析 求出正六棱锥的高,再利用勾股定理求出球的半径,即可求出球的体积.
解答 解:设球的半径是R,则
∵正六棱锥的侧棱长与底面边长分别为$2\sqrt{2}$和2,
∴正六棱锥的高为2,
由题意,R2=22+(R-2)2,
∴R=2,
∴球的体积为$\frac{4}{3}π{R}^{3}$=$\frac{4}{3}π×{2}^{3}$=$\frac{32}{3}π$,
故答案为:$\frac{32}{3}π$.
点评 本题考查求球的体积,考查学生的计算能力,求出球的半径是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.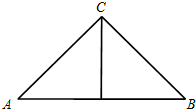 如图,正三棱锥的主视图由等腰直角三角形ABC及斜边AB上的高组成,如果AB=2$\sqrt{3}$,那么这个正三棱锥的体积是( )
如图,正三棱锥的主视图由等腰直角三角形ABC及斜边AB上的高组成,如果AB=2$\sqrt{3}$,那么这个正三棱锥的体积是( )
 如图,正三棱锥的主视图由等腰直角三角形ABC及斜边AB上的高组成,如果AB=2$\sqrt{3}$,那么这个正三棱锥的体积是( )
如图,正三棱锥的主视图由等腰直角三角形ABC及斜边AB上的高组成,如果AB=2$\sqrt{3}$,那么这个正三棱锥的体积是( )| A. | $3\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 9 | D. | 3 |
15.若向量$\overrightarrow{a}$=(sin(α+$\frac{π}{6}$),1),$\overrightarrow{b}$=(1,cosα-$\frac{\sqrt{3}}{4}$),$\overrightarrow{a}$⊥$\overrightarrow{b}$,则sin(α+$\frac{4π}{3}$)=( )
| A. | -$\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
 如图,在多面体ABC-A1B1C1中,AB>A1B1,给出如下两个命题:命题甲:AB∥A1B1,BC∥B1C1;命题乙:多面体ABC-A1B1C1是棱台.试问:从命题甲能否推出命题乙?反之,结果如何?
如图,在多面体ABC-A1B1C1中,AB>A1B1,给出如下两个命题:命题甲:AB∥A1B1,BC∥B1C1;命题乙:多面体ABC-A1B1C1是棱台.试问:从命题甲能否推出命题乙?反之,结果如何?