题目内容
7．集合A={x|0≤x≤2}，B={x|x2-x＞0}，则A∩B=（ ）| A． | R | B． | （-∞，0）∪（1，2） | C． | ∅ | D． | （1，2] |
分析 根据集合的基本运算进行求解即可．
解答 解：B={x|x2-x＞0}={x|x＞1或x＜0}，
则A∩B={x|1＜x≤2}，
故选：D．
点评 本题主要考查集合的基本运算，比较基础．
练习册系列答案
相关题目
18．
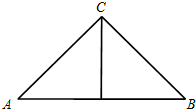如图，正三棱锥的主视图由等腰直角三角形ABC及斜边AB上的高组成，如果AB=2$\sqrt{3}$，那么这个正三棱锥的体积是（ ）
如图，正三棱锥的主视图由等腰直角三角形ABC及斜边AB上的高组成，如果AB=2$\sqrt{3}$，那么这个正三棱锥的体积是（ ）| A． | $3\sqrt{3}$ | B． | $\sqrt{3}$ | C． | 9 | D． | 3 |
15．若向量$\overrightarrow{a}$=（sin（α+$\frac{π}{6}$），1），$\overrightarrow{b}$=（1，cosα-$\frac{\sqrt{3}}{4}$），$\overrightarrow{a}$⊥$\overrightarrow{b}$，则sin（α+$\frac{4π}{3}$）=（ ）
| A． | -$\frac{\sqrt{3}}{4}$ | B． | $\frac{\sqrt{3}}{4}$ | C． | -$\frac{1}{4}$ | D． | $\frac{1}{4}$ |
2．阅读如图所示的程序框图，则该算法最后输出的结果为（ ）
| A． | 15 | B． | 31 | C． | 63 | D． | 127 |
16．为了了解某班同学喜爱打篮球是否与性别有关，对该班全体同学进行了问卷调查，统计调查结果得到如下列联表
已知从该班全体同学中随机抽取1人，抽到喜爱打篮球的学生的概率为$\frac{3}{5}$．
（Ⅰ）求列联表中m，n的值；
（Ⅱ）用分层抽样的方法在喜欢打篮球的同学中抽取6名同学，然后再从这6名同学中任取2名同学，求所选2名同学中至少有1名女生的概率．
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | m | 5 | |
| 女生 | 10 | n | |
| 合计 | 50 |
（Ⅰ）求列联表中m，n的值；
（Ⅱ）用分层抽样的方法在喜欢打篮球的同学中抽取6名同学，然后再从这6名同学中任取2名同学，求所选2名同学中至少有1名女生的概率．
如图是正方体的平面展开图，则在这个正方体中，求证：DE∥平面BCM．