题目内容
9.方程log2x+x=2的解所在的区间为( )| A. | (0.5,1) | B. | (1,1.5) | C. | (1.5,2) | D. | (2,2.5) |
分析 判断f(x)=log2x+x-2,在(0,+∞)上单调递增.根据函数的零点存在性定理得出:f(1)•f(1.5)<0,可得出f(x)的零点在(1,1.5)区间 内,即可得出答案.
解答 解:设f(x)=log2x+x-2,在(0,+∞)上单调递增.
∵f(1)
=0+1-2=-1<0,
f(1.5)=log21.5-0.5=log21.5-log2$\sqrt{2}$>0
∴根据函数的零点存在性定理得出:f(x)的零点在(1,1.5)区间 内
∴方程log2x+x=2的解所在的区间为(1,1.5)
故选:B.
点评 本题考查了函数的单调性,函数零点的判断,方程解所在的区间,属于中档题,但是难度不大,常规题目.

练习册系列答案
相关题目
20.把5名师范大学的毕业生分配到A、B、C三所学校,每所学校至少一人.其中学数学的两人,学语文的两人,学英语的一人,若A校不招收同一学科的毕业生,则不同的分配方法共有( )
| A. | 148种 | B. | 132种 | C. | 126种 | D. | 84种 |
18.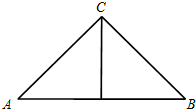 如图,正三棱锥的主视图由等腰直角三角形ABC及斜边AB上的高组成,如果AB=2$\sqrt{3}$,那么这个正三棱锥的体积是( )
如图,正三棱锥的主视图由等腰直角三角形ABC及斜边AB上的高组成,如果AB=2$\sqrt{3}$,那么这个正三棱锥的体积是( )
 如图,正三棱锥的主视图由等腰直角三角形ABC及斜边AB上的高组成,如果AB=2$\sqrt{3}$,那么这个正三棱锥的体积是( )
如图,正三棱锥的主视图由等腰直角三角形ABC及斜边AB上的高组成,如果AB=2$\sqrt{3}$,那么这个正三棱锥的体积是( )| A. | $3\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 9 | D. | 3 |