题目内容
若定义在R上的函数 对任意的
对任意的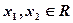 ,都有
,都有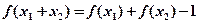 成
成 立,且当
立,且当 时,
时, 。
。
(1)求证: 为奇函数;
为奇函数;
(2)求证: 是R上的增函数;
是R上的增函数;
(3)若 ,解不等式
,解不等式 .
.
 对任意的
对任意的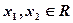 ,都有
,都有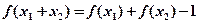 成
成 立,且当
立,且当 时,
时, 。
。(1)求证:
 为奇函数;
为奇函数;(2)求证:
 是R上的增函数;
是R上的增函数;(3)若
 ,解不等式
,解不等式 .
.略
解:(1) 证明:定义在R上的函数
证明:定义在R上的函数 对任意的
对任意的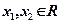 ,都
,都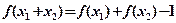 成立。
成立。
令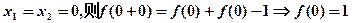
令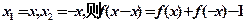 ,∴
,∴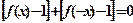 ,∴
,∴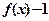 为奇函数
为奇函数
(2)证明:由(1)知: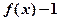 为奇函数, ∴
为奇函数, ∴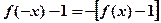
任取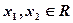 ,且
,且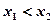 ,则
,则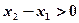 ∵
∵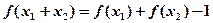
∴
∵当 时,
时,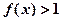 ,
,
∴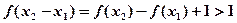 ,∴
,∴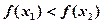
∴ 是R上的增函数。
是R上的增函数。
(3)解:∵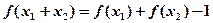 ,且
,且
∴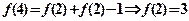 ,由不等式
,由不等式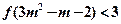 ,
,
得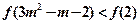
由(2)知: 是R上的增函数∴
是R上的增函数∴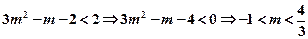
∴不等式 的解集为:
的解集为: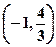
 证明:定义在R上的函数
证明:定义在R上的函数 对任意的
对任意的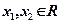 ,都
,都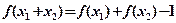 成立。
成立。令
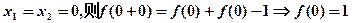
令
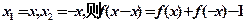 ,∴
,∴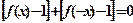 ,∴
,∴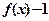 为奇函数
为奇函数(2)证明:由(1)知:
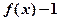 为奇函数, ∴
为奇函数, ∴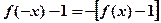
任取
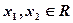 ,且
,且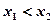 ,则
,则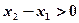 ∵
∵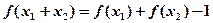
∴

∵当
 时,
时,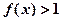 ,
, ∴
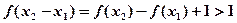 ,∴
,∴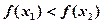
∴
 是R上的增函数。
是R上的增函数。(3)解:∵
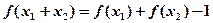 ,且
,且
∴
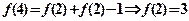 ,由不等式
,由不等式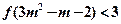 ,
,得
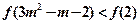
由(2)知:
 是R上的增函数∴
是R上的增函数∴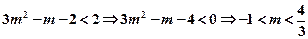
∴不等式
 的解集为:
的解集为: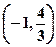

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 与y=x+3
与y=x+3
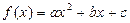 .
.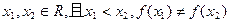 ,方程
,方程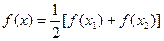 有2个不等实根,
有2个不等实根,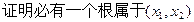 ;
;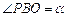 ,求y
,求y 关于
关于 的函数关系式;
的函数关系式; 区的距离之和最小?
区的距离之和最小?
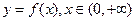 ,如果
,如果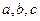 是一个三角形的三边长,那么
是一个三角形的三边长,那么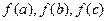 也是一个三角形的三边长,则称函数
也是一个三角形的三边长,则称函数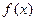 为“保三角形函数”.
为“保三角形函数”.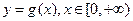 ,如果
,如果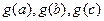 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数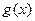 为“恒三角形函数”.
为“恒三角形函数”.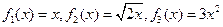 (定义域均为
(定义域均为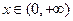 )”中,哪些是“保三角形函数”?请说明理由;
)”中,哪些是“保三角形函数”?请说明理由;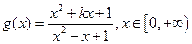 是“恒三角形函数”,试求实数
是“恒三角形函数”,试求实数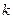 的取值范围;
的取值范围;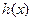 是定义在
是定义在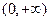 上的周期函数,且值域也为
上的周期函数,且值域也为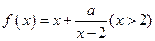 的图象过点A(3,7),则此函的最小值是
的图象过点A(3,7),则此函的最小值是