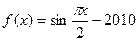题目内容
(本题满分14分)已知二次函数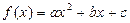 .
.
(1)若a>b>c, 且f(1)=0,证明f(x)的图象与x轴有2个交点;
(2)若 对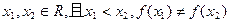 ,方程
,方程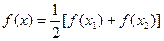 有2个不等实根,
有2个不等实根,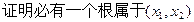 ;
;
(3)在(1)的条件下,是否存在m∈R,使f(m)=-a成立时,f(m+3)为正数,若
存在,证明你的结论,若不存在,说明理由.
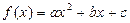 .
.(1)若a>b>c, 且f(1)=0,证明f(x)的图象与x轴有2个交点;
(2)若 对
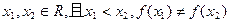 ,方程
,方程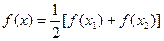 有2个不等实根,
有2个不等实根,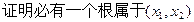 ;
;(3)在(1)的条件下,是否存在m∈R,使f(m)=-a成立时,f(m+3)为正数,若
存在,证明你的结论,若不存在,说明理由.
(1)略(2)略(3)即存在这样的实数m使f(m)=-a成立时,f(m+3)为正数.
解: (1)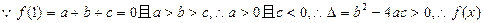 的图象与x轴有两个交点.
的图象与x轴有两个交点.
(2)令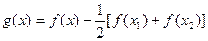 ,则
,则 是二次函数.
是二次函数.
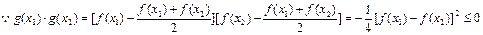
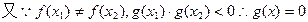 的根必有一个属于
的根必有一个属于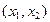 .
.
(3)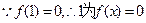 的一个根,由韦达定理知另一根为
的一个根,由韦达定理知另一根为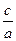 ,1+
,1+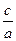 =
=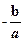 ,
,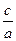 =
=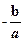 -1
-1

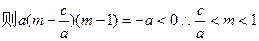
∵ a>b>c,a>0 ∴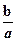 <1 ∴
<1 ∴ 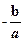 >-1
>-1 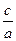 =
=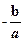 -1>-2
-1>-2
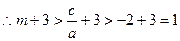 ∵
∵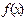 在(1,+∞)单调递增,
在(1,+∞)单调递增,
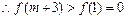 ,即存在这样的实数m使f(m)=-a成立时,f(m+3)为正数.
,即存在这样的实数m使f(m)=-a成立时,f(m+3)为正数.
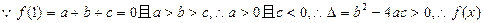 的图象与x轴有两个交点.
的图象与x轴有两个交点.(2)令
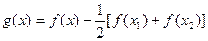 ,则
,则 是二次函数.
是二次函数.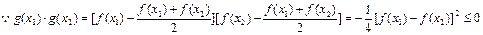
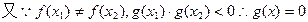 的根必有一个属于
的根必有一个属于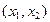 .
.(3)
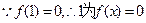 的一个根,由韦达定理知另一根为
的一个根,由韦达定理知另一根为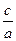 ,1+
,1+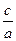 =
=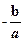 ,
,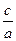 =
=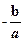 -1
-1
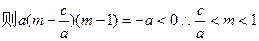
∵ a>b>c,a>0 ∴
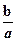 <1 ∴
<1 ∴ 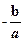 >-1
>-1 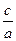 =
=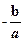 -1>-2
-1>-2 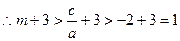 ∵
∵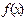 在(1,+∞)单调递增,
在(1,+∞)单调递增,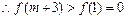 ,即存在这样的实数m使f(m)=-a成立时,f(m+3)为正数.
,即存在这样的实数m使f(m)=-a成立时,f(m+3)为正数.
练习册系列答案
相关题目
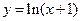
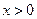 ,证明
,证明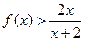 ;
;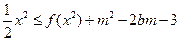 时
时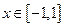 和
和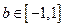 都恒成立,求实数
都恒成立,求实数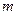 的取值范围。
的取值范围。 对任意的
对任意的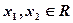 ,都有
,都有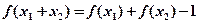 成
成 立,且当
立,且当 时,
时, 。
。 为奇函数;
为奇函数; 是R上的增函数;
是R上的增函数; ,解不等式
,解不等式 .
. 满足条件
满足条件 ,且函数
,且函数 是奇函数,由下列四个命题中不正确的是 ( )
是奇函数,由下列四个命题中不正确的是 ( ) 的图象关于点
的图象关于点 对称
对称 对轴
对轴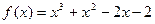 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下: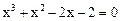 的一个近似根(精确到0.1)为( ).
的一个近似根(精确到0.1)为( ).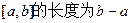 ,区间
,区间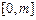 在映射
在映射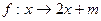 所得的对应区间为
所得的对应区间为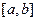 ,若区间
,若区间
 的定义域为
的定义域为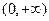
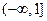
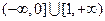
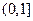
 ,
,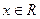 ,有下列4个命题:
,有下列4个命题: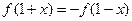 ,则
,则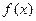 的图象自身关于点
的图象自身关于点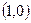 对称;
对称;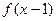 与
与 的图象关于直线
的图象关于直线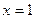 对称;
对称;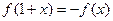 ,则
,则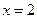 对称;
对称;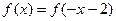 ,则
,则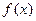 的图像恰好通过
的图像恰好通过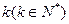 个格点,则称函数
个格点,则称函数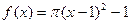 ②
②
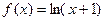 ④
④