题目内容
【题目】在平面直角坐标系中,![]() 为坐标原点,已知向量
为坐标原点,已知向量![]() ,又点
,又点![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求向量
,求向量![]() ;
;
(2)若向量![]() 与向量
与向量![]() 共线,常数
共线,常数![]() ,求
,求![]() 的值域.
的值域.
【答案】(1)![]() 或
或![]() ;(2)当
;(2)当![]() 时
时![]() 的值域为
的值域为![]() .
.
![]() 时
时![]() 的值域为
的值域为![]() .
.
【解析】分析:(1)由已知表示出向量![]() ,再根据
,再根据![]() ,且
,且![]() ,建立方程组求出
,建立方程组求出![]() ,即可求得向量
,即可求得向量![]() ;
;
(2)由已知表示出向量![]() ,结合向量
,结合向量![]() 与向量
与向量![]() 共线,常数
共线,常数![]() ,建立
,建立![]() 的表达式,代入
的表达式,代入![]()
![]() ,对
,对![]() 分类讨论,综合三角函数和二次函数的图象与性质,即可求出
分类讨论,综合三角函数和二次函数的图象与性质,即可求出![]() 值域.
值域.
详解:(1)![]() ,∵
,∵![]() ,且
,且![]() ,
,
∴![]() ,
,![]() ,
,
解得![]() ,
,![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
∴向量![]() 或
或![]() .
.
(2)![]() ,∵向量
,∵向量![]() 与向量
与向量![]() 共线,常数
共线,常数![]() ,
,
∴![]() ,
,
∴![]()
![]() .
.
①当![]() 即
即![]() 时,当
时,当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
![]() 时,
时,![]() 取得最小值
取得最小值![]() ,此时函数
,此时函数![]() 的值域为
的值域为![]() .
.
②当![]() 即
即![]() 时,当
时,当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
![]() 时,
时,![]() 取得最小值
取得最小值![]() ,此时函数
,此时函数![]() 的值域为
的值域为![]() .
.
综上所述,当![]() 时
时![]() 的值域为
的值域为![]() .
.
![]() 时
时![]() 的值域为
的值域为![]() .
.

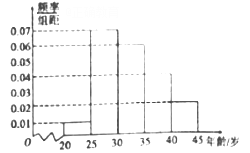
【题目】学校从参加高一年级期中考试的学生中抽出![]() 名学生,并统计了她们的数学成绩(成绩均为整数且满分为
名学生,并统计了她们的数学成绩(成绩均为整数且满分为![]() 分),数学成绩分组及各组频数如下:
分),数学成绩分组及各组频数如下:
![]()
样本频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)在给出的样本频率分布表中,求![]() 的值;
的值;
(2)估计成绩在![]() 分以上(含
分以上(含![]() 分)学生的比例;
分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在![]() 的学生中选两位同学,共同帮助成绩在
的学生中选两位同学,共同帮助成绩在![]() 中的某一位同学.已知甲同学的成绩为
中的某一位同学.已知甲同学的成绩为![]() 分,乙同学的成绩为
分,乙同学的成绩为![]() 分,求甲、乙两同学恰好被安排在同一小组的概率.
分,求甲、乙两同学恰好被安排在同一小组的概率.
【题目】为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满足100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
分组 | 频数 | 频率 |
| 5 | 0.05 |
|
| 0.20 |
| 35 |
|
| 25 | 0.25 |
| 15 | 0.15 |
合计 | 100 | 1.00 |
(1)求![]() 的值并估计这100名考生成绩的平均分;
的值并估计这100名考生成绩的平均分;
(2)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;