题目内容
设数列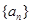 的前n项和为
的前n项和为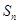 ,已知
,已知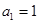 ,
,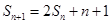
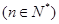 ,
,
(1)求数列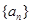 的通项公式;
的通项公式;
(2)若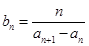 ,数列
,数列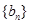 的前n项和为
的前n项和为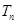 ,
,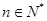 ,证明:
,证明: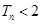 .
.
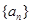 的前n项和为
的前n项和为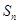 ,已知
,已知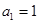 ,
,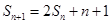
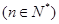 ,
,(1)求数列
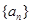 的通项公式;
的通项公式;(2)若
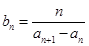 ,数列
,数列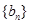 的前n项和为
的前n项和为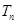 ,
,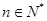 ,证明:
,证明: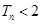 .
.(1)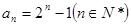 ;(2)证明过程详见解析.
;(2)证明过程详见解析.
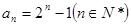 ;(2)证明过程详见解析.
;(2)证明过程详见解析.试题分析:本题主要考查等比数列的通项公式、配凑法求通项公式、错位相减法求和等基础知识,考查学生分析问题解决问题的能力,考查转化能力和计算能力.第一问,已知条件中只有一个等式,利用
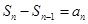 ,用
,用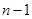 代替式子中的
代替式子中的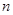 ,得到一个新的表达式,两个式子相减得到
,得到一个新的表达式,两个式子相减得到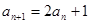 ,再用配凑法,凑出等比数列,求出数列
,再用配凑法,凑出等比数列,求出数列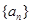 的通项公式;第二问,利用第一问的结论,先化简
的通项公式;第二问,利用第一问的结论,先化简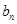 表达式,再利用错位相减法求数列的前n项和,最后的结果与2比较大小.
表达式,再利用错位相减法求数列的前n项和,最后的结果与2比较大小.试题解析:(Ⅰ)∵
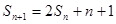 ,当
,当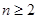 时
时
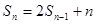
∴
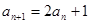 2分
2分∴
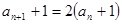 即
即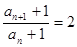 (
(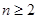 )
) 又
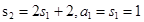 ∴
∴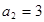 ∴
∴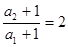
∴
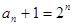 即
即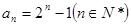 6分
6分(Ⅱ)∵
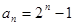 ∴
∴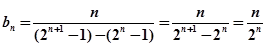 8分
8分∴
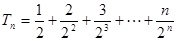 ,
,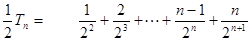
∴
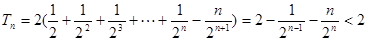 12分
12分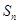 求
求 ;2 配凑法求通项公式;3 等比数列的通项公式;4 错位相减法
;2 配凑法求通项公式;3 等比数列的通项公式;4 错位相减法 
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
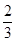 的等比数列{an}的前n项和为Sn,则( )
的等比数列{an}的前n项和为Sn,则( )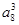 a15=243,则
a15=243,则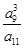 的值为( ).
的值为( ).